题目内容
11.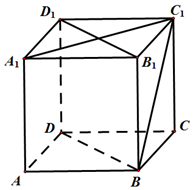 如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;
如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;(1)求证:A1C1⊥平面BB1D1D;
(2)求异面直线B1D1与BC1所成的角.
分析 (1)推导出BB1⊥A1C1,A1C1⊥B1D1,由此能证明A1C1⊥平面BB1D1D.
(2)连结DC1,由B1D1∥BD,知∠DBC1是异面直线B1D1与BC1所成的角,由此能求出异面直线B1D1与BC1所成的角.
解答 证明:(1)∵正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1中,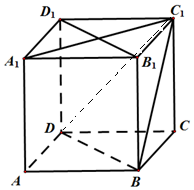
BB1⊥平面A${\;}_{{1}_{\;}}$B1C1D1,A1C1?平面A${\;}_{{1}_{\;}}$B1C1D1,
∴BB1⊥A1C1,∴A1C1⊥B1D1,
又∵B1D1∩BB1=B1,BB1?平面BB1D1D,B1D1?平面BB1D1D,
∴A1C1⊥平面BB1D1D.
解:(2)连结DC1,
∵B1D1∥BD,∴∠DBC1是异面直线B1D1与BC1所成的角,
∵BD=BC1=DC1,
∴∠DBC1=60°,
∴异面直线B1D1与BC1所成的角为60°.
点评 本题线面垂直的证明,考查异面直线所成角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
19.已知复数z=$\frac{{\sqrt{3}+i}}{{1+{i^3}}}$,其中i为虚数单位,则|z|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
6.若圆(x-1)2+(y+1)2=r2上有且只有两个点到直线x-y=1的距离等于$\frac{{\sqrt{2}}}{2}$则半径r的取值范围是( )
| A. | $(0,\sqrt{2}]$ | B. | $(0,\sqrt{2})$ | C. | $[0,\sqrt{2})$ | D. | $[0,\sqrt{2}]$ |
16.已知函数f(x)=x+sinπx,则$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})$=( )
| A. | 4033 | B. | -4033 | C. | 4034 | D. | -4034 |
