题目内容
14.设数列{an}的前n项和为Sn.已知2Sn=3n+3,则{an}的通项公式为${a_n}=\left\{\begin{array}{l}3,\;\;\;\;n=1\\{3^{n-1}},n>1\end{array}\right.$.分析 利用递推关系即可得出,需要验证当n=1时的情况.
解答 解:∵2Sn=3n+3,
∴当n=1时,2a1=3+3,解得a1=3.
当n≥2时,2Sn-1=3n-1+3,
可得2an=3n-3n-1,解得an=3n-1.
∴${a_n}=\left\{\begin{array}{l}3,\;\;\;\;n=1\\{3^{n-1}},n>1\end{array}\right.$,
故答案为:${a_n}=\left\{\begin{array}{l}3,\;\;\;\;n=1\\{3^{n-1}},n>1\end{array}\right.$
点评 本题考查了递推关系的应用、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
15.双曲线的渐近线方程为y=±4x,且焦点在x轴上,则该双曲线的离心率为( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |
5.已知函数f(x)=-x3-x+sinx,若关于x的不等式$f(\frac{1}{x})+f(x-m)>0$在$[\frac{1}{2},2]$上有解,则实数m的取值范围是( )
| A. | $m<\frac{5}{2}$ | B. | $m>\frac{5}{2}$ | C. | m<2 | D. | m>2 |
9.设a=log${\;}_{\frac{1}{3}}}$2,b=20.6,c=log43,则a,b,c的大小关系为( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
6.一个底面为正方形的棱锥的三视图如图所示,则它的外接球的表面积为( )
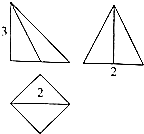

| A. | $\frac{13π}{4}$ | B. | $\frac{{\sqrt{13}π}}{2}$ | C. | 13π | D. | $\sqrt{13}π$ |
3.已知集合A={3,log2(a2+3a)},B={a,b,1},若A∩B={2},则集合A∪B=( )
| A. | {1,2,3,4} | B. | {-4,1,2,3} | C. | {1,2,3} | D. | {-1,4,2} |
4.集合A={x|x2-5x+4<0},B={x||a-x|<1},则“B⊆A”是“a∈(2,3)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |