题目内容
已知cos(
-θ)=
,θ∈(
,π).
(Ⅰ)求cosθ的值;
(Ⅱ)求函数f(x)=
sinxcosx-
sinθcos2x的增区间.
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
(Ⅰ)求cosθ的值;
(Ⅱ)求函数f(x)=
| 3 |
| 5 |
| 6 |
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)直接利用三角函数的诱导公式和同角三角函数的关系式求出结果.
(Ⅱ)对三角函数关系式进行恒等变换,变形成正弦型函数,进一步利用整体思想求出函数函数的单调区间.
(Ⅱ)对三角函数关系式进行恒等变换,变形成正弦型函数,进一步利用整体思想求出函数函数的单调区间.
解答:
(Ⅰ)解:由cos(
-θ)=
,
得sinθ=
,
又sin2θ+cos2θ=1,
所以cos2θ=
因为θ∈(
,π),
所以cosθ=-
(Ⅱ)f(x)=
sinxcosx-
sinθcos2x
=
sinxcosx-
×
cos2x
=
sin2x-
cos2x
=sin(2x-
)
由2kπ-
≤2x-
≤2kπ+
,k∈Z
得kπ-
≤x≤kπ+
,
所以,函数f(x)的增区间是[kπ-
,kπ+
](k∈Z).
| π |
| 2 |
| 3 |
| 5 |
得sinθ=
| 3 |
| 5 |
又sin2θ+cos2θ=1,
所以cos2θ=
| 16 |
| 25 |
因为θ∈(
| π |
| 2 |
所以cosθ=-
| 4 |
| 5 |
(Ⅱ)f(x)=
| 3 |
| 5 |
| 6 |
=
| 3 |
| 5 |
| 6 |
| 3 |
| 5 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得kπ-
| π |
| 6 |
| π |
| 3 |
所以,函数f(x)的增区间是[kπ-
| π |
| 6 |
| π |
| 3 |
点评:本题考查的知识要点:同角三角恒等式的应用,三角函数关系式的恒等变换,利用整体思想求三角函数的单调区间,属于基础题型.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
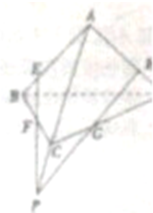

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |