题目内容
14.函数f(x)=x2+x+sinx+cosx+c的图象不过坐标原点,且当x∈[-π,π]时,f(x)的图象不存在关于坐标原点对称的两点,则c可取到的最大负整数是-9.分析 假设f(x)图象上存在两点关于原点对称,设其中一个点横坐标为x,则f(x)+f(-x)=0,x∈(0,π],得出c关于x的函数,求出函数c(x)的值域即c的范围M,则符合条件的c为集合M的补集,得出答案.
解答 解:∵f(x)的图象不过坐标原点,
∴f(0)≠0,即1+c≠0,∴c≠-1.
假设f(x)的图象存在关于坐标原点对称的两点,设两点坐标为(x,f(x)),(-x,-f(x)).x∈(0,π]
则f(x)+f(-x)=0,
∴2x2+2cosx+2c=0,
∴c=-x2-cosx,
∴c′(x)=-2x+sinx<0.
∴c(x)在(0,π]上单调递减,
∴1-π2≤c<-1,
∵f(x)的图象不存在关于坐标原点对称的两点,∴c≥-1或c<1-π2≈-8.87.
又∵c≠-1,
∴c可取到的最大负整数为-9.
故答案为:-9.
点评 本题考查了函数的单调性,函数的值域,属于中档题.

练习册系列答案
相关题目
4.已知直线l与直线2x-y+4=0关于x=1对称,则直线l的方程是( )
| A. | 2x+y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
2.将4个球随机放入3个空盒,则所有球都在两个盒中,但不是全在一个盒子里的概率为( )
| A. | $\frac{7}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{14}{27}$ | D. | $\frac{14}{81}$ |
13.下列函数中满足$f(\frac{{{x_1}+{x_2}}}{2})<\frac{{f({x_1})+f({x_2})}}{2}({x_1}≠{x_2})$的是( )
| A. | f(x)=3x+2 | B. | $f(x)=\sqrt{x}$ | C. | $f(x)=-{(\frac{1}{2})^x}$ | D. | f(x)=x2+x+1 |
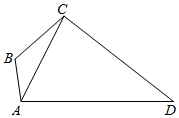 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.