题目内容
13.下列函数中满足$f(\frac{{{x_1}+{x_2}}}{2})<\frac{{f({x_1})+f({x_2})}}{2}({x_1}≠{x_2})$的是( )| A. | f(x)=3x+2 | B. | $f(x)=\sqrt{x}$ | C. | $f(x)=-{(\frac{1}{2})^x}$ | D. | f(x)=x2+x+1 |
分析 可用图表示满足$f(\frac{{x}_{1}+{x}_{2}}{2})<\frac{f({x}_{1})+f({x}_{2})}{2}$的图象,从而由图象看出满足该条件的函数为下凸函数,从而判断每个选项函数的图象是否下凸即可.
解答 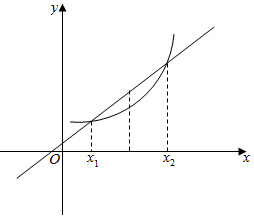 解:如图,
解:如图,
可看出满足$f(\frac{{x}_{1}+{x}_{2}}{2})<\frac{f({x}_{1})+f({x}_{2})}{2}$的函数为下凸函数;
根据每个选项函数的图象便可看出只有选项D的二次函数为下凸函数.
故选:D.
点评 考查满足条件$f(\frac{{x}_{1}+{x}_{2}}{2})<\frac{f({x}_{1})+f({x}_{2})}{2}$的函数为下凸函数,并能够用图象加以说明,中点坐标公式,要熟悉一次函数,二次函数,及指数函数,$y=\sqrt{x}$的图象,以及函数关于x轴的对称变换.

练习册系列答案
相关题目
1.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,F1,F2是椭圆的两个焦点,A为椭圆的右顶点,B为椭圆的上顶点.若在线段AB(不含端点)上存在不同的两个点A1,A2,使得△F1A1F2和△F1A2F2均为以F1F2为斜边的直角三角形,则椭圆的离心率的取值范围为( )
| A. | ($\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{5}-1}{2}$,1) | C. | (0,$\frac{\sqrt{5}-1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,1) |
8.已知集合B={1},C={3},A∪B={1,2},则( )
| A. | A∩B=∅ | B. | A∩C=∅ | C. | A∪C={1,2,3} | D. | A∪C={2,3} |
18.公差为1的等差数列{an}中,a1,a3,a6成等比数列,则{an}的前10项和为( )
| A. | 65 | B. | 80 | C. | 85 | D. | 170 |
2.下列函数中,既是奇函数又在区间(-1,1)上单调递减的函数是( )
| A. | f(x)=sinx | B. | f(x)=2cosx+1 | C. | f(x)=2x-1 | D. | $f(x)=ln\frac{1-x}{1+x}$ |