题目内容
已知a，b，c均为正实数，且a+b+c=12，ab+bc+ca=45，则max{a，b，c}的最小值为 ．
考点：二维形式的柯西不等式
专题：计算题,不等式的解法及应用
分析：不妨设a=Max{a，b，c}，根据条件确定a的不等式，即可求出max{a，b，c}的最小值．
解答：
解：不妨设a=Max{a，b，c}
由a+b+c=12得到a≥4并有（a-b）（a-c）≥0得到关系a2-ab-ac+bc＞=0
即：a2-a（12-a）+bc≥0 即：bc≥12a-2a2，
由45=ab+bc+ac=bc+a（12-a）≥12a-2a2+a（12-a）
∴（a-5）（a-3）≥0
∴a≥5
∴max{a，b，c}的最小值为5．
故答案为：5．
由a+b+c=12得到a≥4并有（a-b）（a-c）≥0得到关系a2-ab-ac+bc＞=0
即：a2-a（12-a）+bc≥0 即：bc≥12a-2a2，
由45=ab+bc+ac=bc+a（12-a）≥12a-2a2+a（12-a）
∴（a-5）（a-3）≥0
∴a≥5
∴max{a，b，c}的最小值为5．
故答案为：5．
点评：本题考查max{a，b，c}的最小值，考查学生分析解决问题的能力，正确转化是关键．
练习册系列答案
相关题目
非零向量
和
满足2|
|=|
|，
⊥（
+
），则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某几何体的三视图，则该几何体的体积等于（ ）
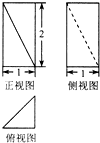
A、
| ||
B、
| ||
| C、1 | ||
D、
|
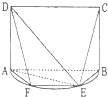如图，E是以AB为直径的半圆O上异于点A，B的点，边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面．
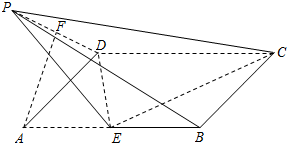如图所示，在矩形ABCD中，AD=1，AB=2，点E是线段AB的中点，把三角形AED沿DE折起，设折起后点A的位置为 P，F是PD的中点．函数y=log
（x2-3x+2）的单调递增区间为（ ）
| 1 |
| 2 |
| A、（-∞，1） | ||
B、（-∞，
| ||
C、[
| ||
| D、（2，+∞） |
如图是一个几何体的三视图，根据图中数据可得该几何体的体积是（ ）
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |