题目内容
设f(x)=
,x=f(x)有唯一解,f(x0)=
,f(xn-1)=xn,n=1,2,3,…,则x2015= .
| x |
| a(x+2) |
| 1 |
| 1008 |
考点:进行简单的演绎推理
专题:综合题,推理和证明
分析:由已知得f(x)=
,从而xn=f(xn-1)=
,
-
=
,由此能求出数列{
}是首项为1008,公差等于
的等差数列.由此能求出结果.
| 2x |
| x+2 |
| 2xn-1 |
| xn-1+2 |
| 1 |
| xn |
| 1 |
| xn-1 |
| 1 |
| 2 |
| 1 |
| xn |
| 1 |
| 2 |
解答:
解:∵f(x)=
,f(x)=x有唯一解,
∴x=
,解得x=0或x=
-2,
由题意知
-2=0,∴a=
,f(x)=
,
∴xn=f(xn-1)=
,
∴
-
=
,
又∵x1=f(x0)=
,∴
=1008,
∴数列{
}是首项为1008,公差等于
的等差数列.
∴
=1008+(2015-1)•
=2015,
∴x2015=
.
故答案为:
.
| x |
| a(x+2) |
∴x=
| x |
| a(x+2) |
| 1 |
| a |
由题意知
| 1 |
| a |
| 1 |
| 2 |
| 2x |
| x+2 |
∴xn=f(xn-1)=
| 2xn-1 |
| xn-1+2 |
∴
| 1 |
| xn |
| 1 |
| xn-1 |
| 1 |
| 2 |
又∵x1=f(x0)=
| 1 |
| 1008 |
| 1 |
| x1 |
∴数列{
| 1 |
| xn |
| 1 |
| 2 |
∴
| 1 |
| x2015 |
| 1 |
| 2 |
∴x2015=
| 1 |
| 2015 |
故答案为:
| 1 |
| 2015 |
点评:本题考查函数值的求法,解题时要认真审题,注意函数性质和等差数列的性质的合理运用.

练习册系列答案
相关题目
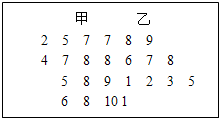 在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格. 如图是一个算法流程图,则输出的x的值是
如图是一个算法流程图,则输出的x的值是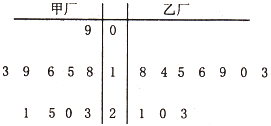 为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如图所示:规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.
为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如图所示:规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品.