题目内容
给出定理“圆内接四边形的对角互补”,根据定理求解:k为何值时,直线l:x+3y-7=0和l:kx-y-2=0与x轴y轴所围成的四边形有外接圆?并求此外接圆的标准方程.
考点:圆的标准方程
专题:计算题,直线与圆
分析:两直线与两坐标轴围成的四边形有外接圆,得到两直线垂直,即斜率的乘积为-1,求出k的值,求出圆的半径,写出圆的标准方程即可.
解答:
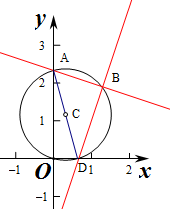 解:若两线x+3y-7=0 与kx-y-2=0于两坐标轴围成的四边形有外接圆,
解:若两线x+3y-7=0 与kx-y-2=0于两坐标轴围成的四边形有外接圆,
∵坐标轴的夹角为90°,
∴两直线两线x+3y-7=0 与kx-y-2=0垂直,即-
k=-1,
解得:k=3,
即3x-y-2=0,此时直线与x轴的交点坐标为D(
,0),
直线x+3y-7=0与y轴的交点坐标为A(0,
),
则A,B的中点坐标即外接圆的圆心坐标为C(
,
),
半径为
|AD|=
,
则此外接圆的方程为(x-
)2+(y-
)2=
.
 解:若两线x+3y-7=0 与kx-y-2=0于两坐标轴围成的四边形有外接圆,
解:若两线x+3y-7=0 与kx-y-2=0于两坐标轴围成的四边形有外接圆,∵坐标轴的夹角为90°,
∴两直线两线x+3y-7=0 与kx-y-2=0垂直,即-
| 1 |
| 3 |
解得:k=3,
即3x-y-2=0,此时直线与x轴的交点坐标为D(
| 2 |
| 3 |
直线x+3y-7=0与y轴的交点坐标为A(0,
| 7 |
| 3 |
则A,B的中点坐标即外接圆的圆心坐标为C(
| 1 |
| 3 |
| 7 |
| 6 |
半径为
| 1 |
| 2 |
| ||
| 6 |
则此外接圆的方程为(x-
| 1 |
| 3 |
| 7 |
| 6 |
| 53 |
| 36 |
点评:本题主要考查圆的标准方程,根据条件求出k,确定出圆心与半径是解本题的关键.

练习册系列答案
相关题目
已知正项等比数列{an}中,Sn为其前n项和,且a2a4=1,S3=7则S5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x+
=-1,则
的值为( )
| 1 |
| x |
| (1-x+x2)(1-x2+x4) |
| x3 |
| A、-1 | B、0 | C、2 | D、4 |