题目内容
12.数列{an}的各项均为正数,Sn为其前n项和,且对任意的n∈N*,均有2an,2Sn,$a_n^2$成等差数列.(1)求a1的值;
(2)求数列{an}的通项公式.
分析 (1)由已知可得$4{S}_{n}=2{a}_{n}+{{a}_{n}}^{2}$,取n=1,化为关于a1的一元二次方程求得a1的值;
(2)对于n≥1,有$4{S_n}=2{a_n}+a_n^2$,因此$4{S_{n-1}}=2{a_{n-1}}+a_{n-1}^2,n≥2$,两式作差后可得{an}是公差为2,首项为2的等差数列,则数列{an}的通项公式可求.
解答 解:(1)∵2an,2Sn,$a_n^2$成等差数列,
∴$4{S}_{n}=2{a}_{n}+{{a}_{n}}^{2}$,
当n=1时,有$4{S_1}=2{a_1}+a_1^2$,即$4{a_1}=2{a_1}+a_1^2$.
∴a1(a1-2)=0,
由于a1>0,故a1=2;
(2)对于n≥1,有$4{S_n}=2{a_n}+a_n^2$,①
因此$4{S_{n-1}}=2{a_{n-1}}+a_{n-1}^2,n≥2$ ②
由①-②得,$4{a_n}=2{a_n}-2{a_{n-1}}+a_n^2-a_{n-1}^2$.
即2(an+an-1)=(an+an-1)(an-an-1).
由于an和an-1均为正数,故an-an-1=2,n≥2.
从而{an}是公差为2,首项为2的等差数列.
因此,an=2n,n≥1.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.

练习册系列答案
相关题目
3.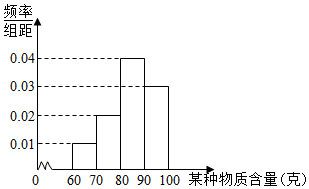 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
(I)估计产品中该物质含量的平均数及方差(同一组数据用该区间的中点值作代表);
(Ⅱ)规定产品的级别如表:
现质检部门从三个等级的产品中采用分层抽样的方式抽取10件产品,再从中随机抽取3件产品进行检测,记质检部门“抽到B或C级品的个数为ξ”,求ξ的分布列和数学期望.
 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.(I)估计产品中该物质含量的平均数及方差(同一组数据用该区间的中点值作代表);
(Ⅱ)规定产品的级别如表:
| 产品级别 | C | B | A |
| 某押麴质含量范围 | [60,70) | [70,80) | [80,100] |
20.已知不等式2x+m+$\frac{8}{x-1}$>0对一切x∈(1,+∞)恒成立,则实数m的取值范围是( )
| A. | m>-10 | B. | m<-10 | C. | m>-8 | D. | m<-8 |
7.数列{an}前n项和${S_n}={2^n}$,则an=$\left\{{\begin{array}{l}{2,n=1}\\{{2^{n-1}},n≥2}\end{array}}\right.$.
1.在数列{an}中,an+1-an=2,Sn为{an}的前n项和.若S10=50,则数列{an+an+1}的前10项和为( )
| A. | 100 | B. | 110 | C. | 120 | D. | 130 |