题目内容
4.已知各项均为正数的等比数列{an}的前三项为a-2,4,2a,记前n项和为Sn.(1)设Sk=62,求a和k的值;
(2)令bn=(2n-1)an,求数列{bn}的前n项和Tn.
分析 (1)利用等比数列的通项公式及其前n项和公式即可得出;
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵各项均为正数的等比数列{an}的前三项为a-2,4,2a,
∴42=2a(a-2),化为a2-2a-8=0,解得a=4或-2.
∵a>0,∴a=4.
∴a1=2,a2=4,公比q=$\frac{4}{2}$=2.
∴Sk=62=$\frac{2({2}^{k}-1)}{2-1}$,解得k=5.
∴a=4,k=5.
(2)由(1)可得:an=2n.
bn=(2n-1)an=(2n-1)•2n.
∴数列{bn}的前n项和Tn=2+3×22+5×23+…+(2n-1)•2n,
∴2Tn=22+3×23+…+(2n-3)•2n+(2n-1)•2n+1,
∴-Tn=2+2(22+23+…+2n)-(2n-1)•2n+1=$\frac{4({2}^{n}-1)}{2-1}$-2-(2n-1)•2n+1=(3-2n)•2n+1-6,
∴Tn=(2n-3)•2n+1+6.
点评 本题考查了等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.某几何体的三视图如图所示,且该几何体的体积是$\frac{3}{2}$,则正视图中的x的值是( )
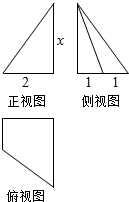

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
19.已知函数f(x)=x2(ex+e-x)-(2x+1)2(e2x+1+e-2x-1),则满足f(x)>0的实数x的取值范围为( )
| A. | (-1,-$\frac{1}{3}$) | B. | (-∞,-1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
9.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(1-x)(x<0)}\\{g(x)+1(x>0)}\end{array}\right.$,若f(x)是奇函数,则g(3)的值是( )
| A. | 1 | B. | 3 | C. | -3 | D. | -1 |
16.定义在R上的函数f(x)满足f(x+1)=2f(x),且当0≤x≤1时,f(x)=x2-x,则$f({-\frac{3}{2}})$=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{1}{16}$ |