题目内容
9.在Rt△ABC中,∠C=90°,AC=6,BC=4,点D满足$\overrightarrow{AD}$=-2$\overrightarrow{DB}$,若以直角顶点C为坐标原点,CB,CA所在直线为x轴、y轴建立直角坐标系,则$\overrightarrow{CD}$的坐标为($\frac{8}{3}$,2).分析 根据题意,画出图形,结合图形,设出点D的坐标,利用平面向量的坐标表示,列出方程组求出点D的坐标即可.
解答 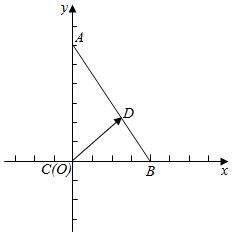 解:如图所示,
解:如图所示,
Rt△ABC中,∠C=90°,AC=6,BC=4,
∴B(4,0),A(0,6);
设D(x,y),
则$\overrightarrow{AD}$=(x,y-6),$\overrightarrow{DB}$=(x-4,y),
又点D满足$\overrightarrow{AD}$=-2$\overrightarrow{DB}$,
∴$\left\{\begin{array}{l}{x=-2(x-4)}\\{y-6=-2y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=2}\end{array}\right.$,
∴点D($\frac{8}{3}$,2),
∴$\overrightarrow{CD}$=($\frac{8}{3}$,2).
故答案为:($\frac{8}{3}$,2).
点评 本题考查了平面向量的坐标表示与运算问题,也考查了解方程组的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )
 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
1.“xy≠0”是“x≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |