题目内容
19. 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象如图所示,则f($\frac{π}{4}$)等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式,从而求得求f($\frac{π}{4}$)的值.
解答 解:由函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0),|φ|<$\frac{π}{2}$的部分图象,
可得A=1,$\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{3}$+$\frac{π}{6}$,求得ω=2,再根据五点法作图可得2•(-$\frac{π}{6}$)+φ=0,
求得φ=$\frac{π}{3}$,故f(x)=sin(2x+$\frac{π}{3}$),f($\frac{π}{4}$)=sin($\frac{π}{2}$+$\frac{π}{3}$)=cos$\frac{π}{3}$=$\frac{1}{2}$,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,求函数的值,属于基础题.

练习册系列答案
相关题目
11.若a,b,c>0且(a+b)(a+c)=4-2$\sqrt{3}$,则2a+b+c的最小值为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$+2 | D. | 2$\sqrt{3}$-2 |
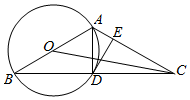 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.