题目内容

已知△ABC中，AB=2，AC=4，O为△ABC的外心，则
AO
•
BC
等于（　　）
A、4B、6C、8D、10
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量数量积的几何意义和三角形外心的性质即可得出．
解答： 解：结合向量数量积的几何意义及点O在线段AB，AC上的射影为相应线段的中点，
可得
AO
•
AB
=
|
AB
|2
2
=2，
AO
•
AC
=
|
AC
|2
2
=8，
∴
AO
•
BC
=
AO
•
AC
-
AO
•
AB
=8-2=6，
故选：B，
点评：本题考查了向量数量积的几何意义和三角形外心的性质、向量的三角形法则，属于中档题．
练习册系列答案
相关题目
持续性的雾霾天气严重威胁着人们的身体健康，汽车的尾气排放是造成雾霾天气的重要因素之一．为此，某城市实施了机动车尾号限行，该市报社调查组为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：
年龄（岁） [15，25） [25，35） [35，45） [45，55） [55，65） [65，75]
频数 5 10 15 10 5 5
赞成人数 4 6 9 6 3 4
（Ⅰ）请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值；
（Ⅱ）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行追踪调查，记被选4人中不赞成“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望；
（Ⅲ）若在这50名被调查者中随机发出20份的调查问卷，记η为所发到的20人中赞成“车辆限行”的人数，求使概率P（η=k）取得最大值的整数k．
若实数x，y满足1+cos2πx=
(x+2y)2+1
x+2y
，则x2+（y+1）2的最小值为
 
．
执行如图的程序，输出的正整数n的值为
 
．
如图给出的是计算1+
1
3
+
1
5
+…+
1
11
的值的一个程序框图，其中判断框内应填入的条件是（　　）
A、i＜12B、i＞11
C、i＜11D、i≤6
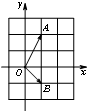如图，在复平面内，若复数z1，z2对应的向量分别是
OA
，
OB
，则复数z1+z2所对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知集合A={-1，0，1}，B={x|x+1＞0}，那么A∩B等于（　　）
A、{0，1}
B、{-1，0，1}
C、（-1，+∞）
D、[-1，+∞）
阅读如图所示的程序框图，运行相应的程序．若输入的x∈[0，2），则输出的结果可能是（　　）
A、-1B、0C、1.5D、3
已知函数f（x）=λx（1-x）（λ＞0，x∈[0，1]），若1，sinα，f（sin
α
2
）2成等比数列．
（1）求λ的值；
（2）试探求函数g（x）=f（cos
x
2
）2的性质．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网