题目内容

若M为圆C：x2+y2+6x-4y+12=0上的动点，抛物线E：y2=4x的准线为l，点P是抛物线E上的任意一点，记点P到l的距离为d，则d+|PM|的最小值为
 
．
考点：抛物线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：先根据抛物线方程求得焦点坐标，根据圆的方程求得圆心坐标，根据抛物线的定义可知P到准线的距离等于点P到焦点的距离，进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值，根据图象可知当P，Q，F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小，为圆心到焦点F的距离减去圆的半径．
解答： 解：抛物线y2=4x的焦点为F（1，0），圆x2+y2+6x-4y+12=0的圆心为C（-3，2），
根据抛物线的定义可知点P到准线的距离等于点P到焦点的距离，
进而推断出当P，M，F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小为：2
5
-1，
故答案为：2
5
-1．
点评：本题主要考查了抛物线的应用．考查了学生转化和化归，数形结合等数学思想．
练习册系列答案
相关题目
已知某几何体的三视图，根据图中标出的尺寸，可得这个几何体的体积是（　　）
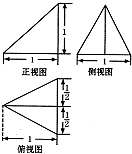
A、
1
12
B、
1
4
C、
1
6
D、
1
3
若非空集合S⊆{1，2，3，4，5}满足若a∈S，则6-a∈S，写出这样的所有S．
已知数列{an}中，
a
 
1
=
1
4
，an=2-
1
an-1
(n≥2，n∈N*)．若数列{bn}满足bn=
1
an-1
(n∈N+)．
（1）证明：数列{bn}是等差数列，并写出{bn}的通项公式；
（2）求数列{an}的通项公式及数列{an}中的最大项与最小项．
已知椭圆γ：
x2
4
+y2=1的右焦点为F，左顶点为R，点A（2，1），B（-2，1），O为坐标原点．
（1）若P是椭圆γ上任意一点，
OP
=m
OA
+n
OB
，求m2+n2的值；
（2）设Q是椭圆γ上任意一点，S（t，0），t∈（2，5），求
QS
•
QR
的取值范围；
（3）过F作斜率为k的直线l交椭圆γ于C，D两点，交y轴于点E，若
EC
=λ1
CF
，
ED
=λ2
DF
，试探究λ1+λ2是否为定值，说明理由．
圆锥的底面半径为3，高为1，则圆锥的侧面积为
 
．
对于大或等于2的正整数m的n次方幂有如下分解方式：

根据上述分解规律．若m3（m∈N*）的分解中最小的数是91，则m的值为
 
．
函数y=f（x）是定义在R上的奇函数且y=f（x+1）也是奇函数，若f（3）=0，则函数y=f（x）在区间（0，8）内的零点个数至少有（　　）
A、4B、5C、6D、7
一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的体积为（　　）
A、
4π
3
B、
8π
3
C、4π
D、8π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网