题目内容
已知F1、F2为椭圆C：
+y2=1 的左、右焦点，点P在椭圆C上，∠F1PF2=60°，则|PF1|•|PF2|= ．
| x2 |
| 4 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用余弦定理及椭圆的定义，解方程求|PF1|•|PF2|的值．
解答：
解：∵椭圆方程为
+y2=1，
∴a=2，b=1，c=
．
设|PF1|=m，|PF2|=n，则m+n=4①，
由余弦定理得，12=m2+n2-2mncos60°=m2+n2-mn②，
①2-②，可得|PF1|•|PF2|=mn=
，
故答案为：
．
| x2 |
| 4 |
∴a=2，b=1，c=
| 3 |
设|PF1|=m，|PF2|=n，则m+n=4①，
由余弦定理得，12=m2+n2-2mncos60°=m2+n2-mn②，
①2-②，可得|PF1|•|PF2|=mn=
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题主要考查椭圆定义、几何性质、余弦定理，考查转化的数学思想，查考生的综合运用能力及运算能力．
练习册系列答案
相关题目
过点（1，3）且斜率为3的直线方程为（ ）
| A、y-3=3（x-1） |
| B、y-3=3（x+1） |
| C、y+3=3（x-1） |
| D、y+3=3（x+1） |
设P和Q是两个集合，定义集合P-Q={x|x∈P，且x∉Q}，如果P={x|log2x＜1}，{x||x-2|＜1}，那么P-Q=（ ）
| A、{x|0＜x＜1} |
| B、{x|x＜x≤1} |
| C、{x|1≤x＜2} |
| D、{x|2≤x＜3} |
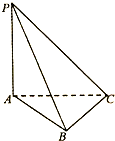如图，在三棱锥P-ABC中，已知△ABC是等腰直角三角形，∠ABC=90°，△PAC是直角三角形，∠PAC=90°，∠ACP=30°，平面PAC⊥平面ABC．
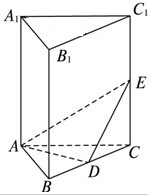已知在直三棱柱ABC-A1B1C1中，E为CC1上任意一点，D在BC上（点D不同于点C），AD⊥DE，求证：平面ADE⊥平面BCC1B1．