题目内容
5.集合A={1,2,4},B={x|x2∈A},将集合A、B分别用如图中的两个圆表示,则圆中阴影部分表示的集合中元素个数恰好为4的是( )| A. | 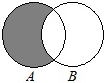 | B. | 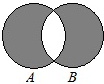 | C. | 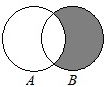 | D. |  |
分析 根据集合的基本运算和关系进行判断即可.
解答 解:∵A={1,2,4},B={x|x2∈A},
∴B={1,-1,$\sqrt{2}$,-$\sqrt{2}$,2,-2},
则A∩B={1,2},A∪B={1,-1,$\sqrt{2}$,-$\sqrt{2}$,2,-2,4},
A.元素x∈A且x∉B,即x∈{4},故A错误,
B.x∈A∪B且x∉A∩B,即x∈{-1,$\sqrt{2}$,-$\sqrt{2}$,-2,4},故B错误,
C.元素x∈B且x∉A,即x∈∈{-1,$\sqrt{2}$,-$\sqrt{2}$,-2,}有4个元素,故C正确,
D..x∈A∩B,即x∈{1,2},故D错误,
故选:C
点评 本题主要考查集合的基本运算和关系,比较基础.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
20.若x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x≤y}\\{x+y≤4}\end{array}\right.$,则$\frac{1}{x}$+$\frac{2}{y}$的最大值为( )
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
10.在区间[0,2π]上随机取一个数x,则事件“cosx≥$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{11}{12}$ |
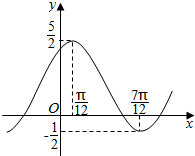 函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.