题目内容
17.在空间中,以AB为公共边的两正方形ABCD,ABEF的边长皆为4,已知$\overrightarrow{AD}$•$\overrightarrow{AF}$=2,则$\overrightarrow{AC}$•$\overrightarrow{AE}$=( )| A. | 18 | B. | 14 | C. | 30 | D. | 34 |
分析 作出图形,求出二面角的大小,EC,AE,AC,使用余弦定理求出$\overrightarrow{AE},\overrightarrow{AC}$的夹角,代入数量积公式计算.
解答 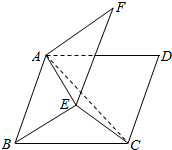 解:∵$\overrightarrow{AD}$•$\overrightarrow{AF}$=4×4×cos∠DAF=2,∴cos∠DAF=$\frac{1}{8}$.∴cos∠CBE=cos∠DAF=$\frac{1}{8}$.
解:∵$\overrightarrow{AD}$•$\overrightarrow{AF}$=4×4×cos∠DAF=2,∴cos∠DAF=$\frac{1}{8}$.∴cos∠CBE=cos∠DAF=$\frac{1}{8}$.
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}-2BC•BEcos∠CBE}$=2$\sqrt{7}$.
∵AC=AE=4$\sqrt{2}$,∴cos∠CAE=$\frac{A{C}^{2}+A{E}^{2}-C{E}^{2}}{2AC•AE}$=$\frac{9}{16}$.
∴$\overrightarrow{AC}$•$\overrightarrow{AE}$=AC•AE•cos∠CAE=4$\sqrt{2}$×4$\sqrt{2}$×$\frac{9}{16}$=18.
故选:A.
点评 本题考查了平面向量的数量积运算,余弦定理的应用,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
7.设a,b,c大于0,a+b+c=3,则3个数:a+$\frac{1}{b}$,b+$\frac{1}{c}$,c+$\frac{1}{a}$的值( )
| A. | 都大于2 | B. | 至少有一个不大于2 | ||
| C. | 都小于2 | D. | 至少有一个不小于2 |
8.甲命题:若随机变量ξ~N(3,σ2),若P(ξ≤2)=0.3,则P(ξ≤4)=0.7.乙命题:随机变量η-B(n,p),且Eη=300,Dη=200,则P=$\frac{1}{3}$,则正确的是( )
| A. | 甲正确乙错误 | B. | 甲错误乙正确 | C. | 甲错误乙也错误 | D. | 甲正确乙也正确 |
6.已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.则下列条件中一定能使得l1∥l2成立的是( )
| A. | m=4 | B. | m=0 | C. | m=4或m=-4 | D. | m=4且n≠-2 |