题目内容
1.△ABC中,sin(A-B)=sinC-sinB,D是边BC的一个三等分点(靠近点B),记$\frac{sin∠ABD}{sin∠BAD}=λ$,则当λ取最大值时,tan∠ACD=2+$\sqrt{3}$.分析 由sin(A-B)=sinC-sinB,得sinB=2cosAsinB,cosA=$\frac{1}{2}$,可得:A=$\frac{π}{3}$,由已知得$\frac{AD}{DB}=λ,即AD=λDB=\frac{1}{3}λa$,利用${\overrightarrow{AD}}^{2}=(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})^{2}$和a2=b2+c2-bc可得λ取最值时,a、b、c间的数量关系.
解答  解:∵sin(A-B)=sinC-sinB,
解:∵sin(A-B)=sinC-sinB,
∴sinAcosB-cosAsinB=sinC-sinB=sinAcosB+cosAsinB-sinB,
∴sinB=2cosAsinB,∵sinB≠0,
∴cosA=$\frac{1}{2}$,由A∈(0,π),可得:A=$\frac{π}{3}$,
在△ADB中,由正弦定理可将$\frac{sin∠ABD}{sin∠BAD}=λ$,变形为则$\frac{AD}{DB}=λ,即AD=λDB=\frac{1}{3}λa$,
∵$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AC})=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$
∴${\overrightarrow{AD}}^{2}=(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})^{2}$即a2λ2=4c2+b2+2bc…①
在△ACB中,由余弦定理得:a2=b2+c2-bc…②
由①②得${λ}^{2}=\frac{4\frac{c}{b}+\frac{b}{c}+2}{\frac{c}{b}+\frac{b}{c}-1}$
令$\frac{c}{b}=t\\;(t>0)$,${λ}^{2}=f(t)=\frac{4t+\frac{1}{t}+2}{t+\frac{1}{t}-1}=\frac{4{t}^{2}+2t+1}{{t}^{2}-t+1}$,f′(t)=$\frac{-6{t}^{2}+6t+3}{({t}^{2}-t+1)^{2}}$,令f′(t)=0,得t=$\frac{1+\sqrt{3}}{2}$,
即$\frac{c}{b}=\frac{1+\sqrt{3}}{2}$时,λ最大.
结合②可得b=$(\sqrt{3}-1)c$,a=$\frac{3\sqrt{2}-\sqrt{6}}{2}$c
在△ACB中,由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}$⇒$sinC=\frac{\sqrt{6}+\sqrt{2}}{4}$,⇒tanC=2+$\sqrt{3}$
故答案为:2+$\sqrt{3}$.
点评 本题考查了正余弦定理的应用,充分体现了函数、方程的思想,运算量较大,属于难题.

 53随堂测系列答案
53随堂测系列答案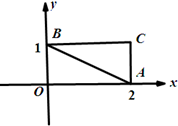 已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).
已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).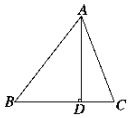 如图所示,在△ABC中,AD⊥BC于D,下列条件:
如图所示,在△ABC中,AD⊥BC于D,下列条件: