题目内容
设椭圆方程为
+
=1,过原点且倾斜角为θ和π-θ(0<θ<
)的两直线分别交椭圆于A,C和B,D两点.
(1)用θ表示四边形ABCD的面积S;
(2)当θ∈(0,
)时,求S的最大值.
| x2 |
| 4 |
| y2 |
| 8 |
| π |
| 2 |
(1)用θ表示四边形ABCD的面积S;
(2)当θ∈(0,
| π |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)设出直线过原点且倾斜角为θ的直线的方程和椭圆方程联立即可表示出四边形ABCD的面积;
(2)根据(1)求得的面积S的函数求其最大值即可.
(2)根据(1)求得的面积S的函数求其最大值即可.
解答:
解:设经过原点且倾斜角为θ的直线方程为y=xtanθ,代入
+
=1,
求得x2=
,y2=
,
由对称性可知四边形ABCD为矩形,又由于0<θ<
,
所以四边形ABCD的面积S=4|x||y|=
;
(2)当0<θ<
时,tanθ>0,
设t=tanθ,则S=
=
,(t>0),
设f(t)=
+t,
f′(t)=1-
,
当0<t<
时,f′(t)<0;
当t>
时,f′(t)>0,
因为f(t)在t=
时,取最小值,
所以f(t)min=f(
)=
+
=2
,
所以当tanθ=
时,Smax=8
.
| x2 |
| 4 |
| y2 |
| 8 |
求得x2=
| 32 |
| 8+4tan2θ |
| 32tan2θ |
| 8+4tan2θ |
由对称性可知四边形ABCD为矩形,又由于0<θ<
| π |
| 2 |
所以四边形ABCD的面积S=4|x||y|=
| 32tanθ |
| 2+tan2θ |
(2)当0<θ<
| π |
| 2 |
设t=tanθ,则S=
| 32t |
| 2+t2 |
| 32 | ||
|
设f(t)=
| 2 |
| t |
f′(t)=1-
| 2 |
| t2 |
当0<t<
| 2 |
当t>
| 2 |
因为f(t)在t=
| 2 |
所以f(t)min=f(
| 2 |
| 2 | ||
|
| 2 |
| 2 |
所以当tanθ=
| 2 |
| 2 |
点评:本题主要考查直线和椭圆的相关知识,三角函数的最值问题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
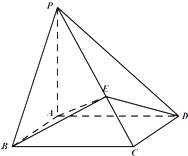 在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=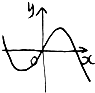
 某班60名同学参加高中数学毕业会考所得成绩(成绩均为整数)整理后画出的频率分布直方图,求该班及格(60分以上)的同学的人数?
某班60名同学参加高中数学毕业会考所得成绩(成绩均为整数)整理后画出的频率分布直方图,求该班及格(60分以上)的同学的人数?