题目内容
设曲线y=sinx上任意一点(x,y)处的切线的斜率为 g(x) 则函数y=x2g(x)的部分图象可以为( )
A、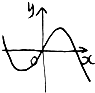 |
B、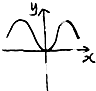 |
C、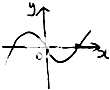 |
D、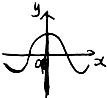 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先根据导数几何意义得到曲线y=sinx上任一点(x,y)处切线斜率g(x),再研究函数y=x2g(x)的奇偶性,再根据在某点处的函数值的符号进一步进行判定.
解答:
解:曲线y=sinx上任一点(x,y)处切线斜率为g(x),
∴g(x)=cosx,则函数y=x2g(x)=x2•cosx,设f(x)=x2•cosx,
则f(-x)=f(x),cos(-x)=cosx,
∴y=f(x)为偶函数,其图象关于y轴对称,排除A、C
令x=0,得f(0)=0.排除D.
故选B
∴g(x)=cosx,则函数y=x2g(x)=x2•cosx,设f(x)=x2•cosx,
则f(-x)=f(x),cos(-x)=cosx,
∴y=f(x)为偶函数,其图象关于y轴对称,排除A、C
令x=0,得f(0)=0.排除D.
故选B
点评:本题主要考查了导数的运算,以及考查学生识别函数的图象的能力,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知f(x)=
则f[f(
)]的值为( )
|
| 2 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
设圆C位于抛物线y2=2x与直线x=3所围成的封闭区域(包括边界)内,则圆的半径能取到的最大值为( )
A、
| ||
B、4-
| ||
C、4+
| ||
D、
|
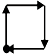
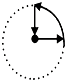
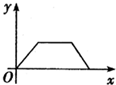 如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )
如图是王珊早晨离开家边走边背诵英语过程中离家距离y与行走时间x之间函数关系的图象.若用黑点表示王珊家的位置,则王珊步行走的路线可能是( )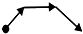

 已知A,B分别是椭圆C:
已知A,B分别是椭圆C: