题目内容
4．
如图，ABCD-A1B1C1D1是正方体，E，F，G，H，M，N分别是所在棱的中点，则下列结论错误的有①③④①GH和MN是平行直线；GH和EF是相交直线
②GH和MN是平行直线；MN和EF是相交直线
③GH和MN是相交直线；GH和EF是异面直线
④GH和EF是异面直线；MN和EF也是异面直线．
分析 根据空间中两条直线的位置关系，对题目中的命题进行分析、判断即可．
解答 解：对于①，GH和MN是平行直线，但GH和EF是异面直线，不是相交直线，∴①错误；
对于②，GH和MN是平行直线；MN和EF是相交直线，并且它们的交点在直线DC上，∴②正确；
对于③，GH和MN是平行直线，不是相交直线；GH和EF是异面直线，∴③错误；
对于④，GH和EF是异面直线；但MN和EF是相交直线，不是异面直线，∴④错误；
综上，错误的命题序号是①③④．
故答案为：①③④．
点评 本题利用正方体为载体考查了空间中两条直线位置关系的判断问题，是基础题目．
练习册系列答案
相关题目
1．在△ABC中，若tanA=$\frac{1}{3}$，tanB=-2，则角C等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
9．设偶函数f（x）满足f（x）=2x-4（x≥0），则{x|f（x-2）＜0}=（ ）
| A． | {x|x＜-2或x＞4} | B． | {x|x＜0或x＞4} | C． | {x|x＜0或x＞6} | D． | {x|0＜x＜4} |
16．若f（x）=x2+2x-3，则f（x）在区间[-2，1]上的值域是（ ）
| A． | [-4，-3] | B． | [-3，0] | C． | [-4，0] | D． | [0，2] |
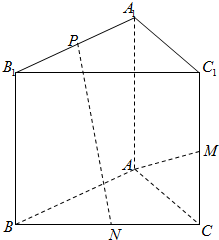已知如图，在直三棱柱ABC-A1B1C1中，AA1=AC，且AB⊥AC，M是面CC1的中点，N是BC的中点，点P在直线A1B1上．
14．数列{an}满足a1=2，${a_{n+1}}=\frac{1}{{1-{a_n}}}（n∈{N^*}）$，则a2016=（ ）
| A． | -2 | B． | -1 | C． | 2 | D． | $\frac{1}{2}$ |