题目内容
点P是底面边长为2
，高为2的正三棱柱表面上一点，MN是该棱柱内切球的一条直径，则
•
的取值范围为 ．
| 3 |
| PM |
| PN |
考点：平面向量数量积的运算
专题：转化思想,平面向量及应用,空间位置关系与距离
分析：根据题意，用平行于底面且过内切球球心的平面截该三棱柱，把问题转化为已知MN是边长为2
的正△ABC内切圆的一条直径，P为边AB上的一动点，求
•
的取值范围建立平面直角坐标系，利用向量的坐标表示求出
•
的取值范围的取值范围．
| 3 |
| PM |
| PN |
| PM |
| PN |
解答：
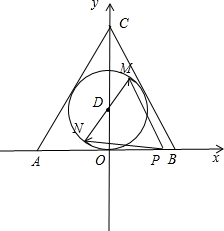解：根据题意，用平行于底面且过内切球球心的平面截该三棱柱，如图所示；
问题转化为已知MN是边长为2
的正△ABC
内切圆的一条直径，P为边AB上的一动点，
求
•
的取值范围；
建立如图所示的直角坐标系，
∵⊙D是边长为2
的正△ABC内切圆，
∴内切圆的半径r=
|OC|=
×
×2
=1，
∴正△ABC内切圆的方程为x2+（y-1）2=1；
设P（t，0）（-
≤t≤
），
M（x0，y0），N（-x0，2-y0），
∴
=（x0-t，y0），
=（-x0-t，2-y0），
∴x02+（y0-1）2=1，即x02+y02-2y0=0；
∴
•
=t2-（x02+y02-2y0）=t2，
∵-
≤t≤
，∴t2∈[0，3]；
∴
•
的取值范围的取值范围是[0，3]．
故答案为：[0，3]．
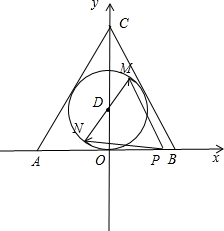解：根据题意，用平行于底面且过内切球球心的平面截该三棱柱，如图所示；问题转化为已知MN是边长为2
| 3 |
内切圆的一条直径，P为边AB上的一动点，
求
| PM |
| PN |
建立如图所示的直角坐标系，
∵⊙D是边长为2
| 3 |
∴内切圆的半径r=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
∴正△ABC内切圆的方程为x2+（y-1）2=1；
设P（t，0）（-
| 3 |
| 3 |
M（x0，y0），N（-x0，2-y0），
∴
| PM |
| PN |
∴x02+（y0-1）2=1，即x02+y02-2y0=0；
∴
| PM |
| PN |
∵-
| 3 |
| 3 |
∴
| PM |
| PN |
故答案为：[0，3]．
点评：本题考查了正三角形的中心、内切圆以及平面向量的数量积的运算等基础知识的应用问题，也考查了转化思想的应用问题，是综合性题目．
练习册系列答案
阅读快车系列答案
相关题目