题目内容
若cos(
-α)=a,则sin(
-α)= .
| π |
| 6 |
| 2π |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:所求式子中的角度变形后,利用诱导公式化简,将已知等式代入计算即可求出值.
解答:
解:∵cos(
-α)=a,
∴sin(
-α)=sin[
+(
-α)]=cos(
-α)=a.
故答案为:a
| π |
| 6 |
∴sin(
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
故答案为:a
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
已知a>0且a≠1,函数f(x)=
满足对任意实数x1≠x2,都有
>0成立,则a的取值范围是( )
|
| f(x2)-f(x1) |
| x2-x1 |
| A、(0,1) | ||
| B、(1,+∞) | ||
C、(1,
| ||
D、[
|
(理)已知z=x+yi,x,y∈R,i是虚数单位.若复数
+i是实数,则|z|的最小值为( )
| z |
| 1+i |
| A、0 | ||
B、
| ||
| C、5 | ||
D、
|
设复数z+i(z为复数)在映射f下的象为zi,则-2+2i的象是( )
| A、2-2i | B、-2-2i |
| C、1-2i | D、-1-2i |
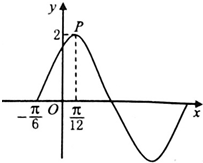 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,