题目内容
12.设二次函数f(x)=x2+ax+b,若对任意的实数a,都存在实数$x∈[{\frac{1}{2},2}]$,使得不等式|f(x)|≥x成立,则实数b的取值范围是( )| A. | $({-∞,-\frac{1}{3}}]∪[{2,+∞}]$ | B. | $({-∞,-\frac{1}{3}}]∪[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{4}}]∪[{\frac{9}{4},+∞})$ | D. | $({-∞,-\frac{1}{3}}]∪[{\frac{9}{4},+∞})$ |
分析 问题转化为只需$g(x)=x+\frac{b}{x},x∈[{\frac{1}{2},2}]$的最大值与最小值之差小于2即可.通过讨论b的范围,求出最大值和最小值的差,从而确定b的范围即可.
解答 解:问题条件的反面为“若存在实数a,对任意实数$x∈[{\frac{1}{2},2}]$,使得不等式|f(x)|<x成立”,
即$?x∈[{\frac{1}{2},2}],-1<x+\frac{b}{x}+a<1$,
只要$g(x)=x+\frac{b}{x},x∈[{\frac{1}{2},2}]$的最大值与最小值之差小于2即可.
当b≥4时,$g(\frac{1}{2})-g(2)<2$,得b∈∅,
当$\frac{1}{4}<b<4$时,$\left\{{\begin{array}{l}{g(2)-2\sqrt{b}<2}\\{g(\frac{1}{2})-2\sqrt{b}<2}\end{array}}\right.$,得$\frac{1}{4}<b<\frac{9}{4}$,
当$b≤\frac{1}{4}$时,$g(2)-g(\frac{1}{2})<2$,得$-\frac{1}{3}<b≤\frac{1}{4}$,
所以,$-\frac{1}{3}<b<\frac{9}{4}$,
综上可得,所求实数b的取值范围是$b≤-\frac{1}{3},或b≥\frac{9}{4}$,
故选:D.
点评 本题考查了二次函数的性质,考查分类讨论思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.2-2的值为( )
| A. | 4 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
2.函数f(x)=Asin(ωx+φ)的部分图象如图所示,若f(4)=-f(6)=-1,且$f(\frac{1}{2})=0$,则f(2017)=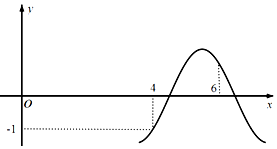

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
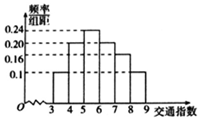 随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示:
随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示: