题目内容
以下命题中，正确的命题为（ ）
A、|
| ||||||||||||||||||
B、（
| ||||||||||||||||||
C、向量
| ||||||||||||||||||
D、在四面体ABCD中，若
|
考点：命题的真假判断与应用
专题：平面向量及应用
分析：A.
、
不共线的充要条件是||
|-|
||＜|
+
|＜|
|+|
|，即可判断；
B．由于向量的数量积是数量，且
，
，
不一定共线，即可判断；
C．由向量的数量积的几何意义和模的概念，即可判断；
D．即为在四面体ABCD中，若AB⊥CD，AC⊥BD，则AD⊥BC．应用线面垂直的判定定理和性质定理，即可判断．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
B．由于向量的数量积是数量，且
| a |
| b |
| c |
C．由向量的数量积的几何意义和模的概念，即可判断；
D．即为在四面体ABCD中，若AB⊥CD，AC⊥BD，则AD⊥BC．应用线面垂直的判定定理和性质定理，即可判断．
解答：
解：A.
、
不共线的充要条件是||
|-|
||＜|
+
|＜|
|+|
|，故A错；
B．由于向量的数量积是数量，且
，
，
不一定共线，故B错；
C．由于
•
=|
|•|
|•cos＜
，
＞，则向量
在向量
方向上的射影向量的模为
||
|•cos＜
，
＞|，故C错；
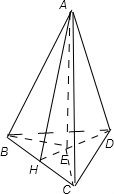
D．即为在四面体ABCD中，若AB⊥CD，AC⊥BD，则AD⊥BC．
如图作AE⊥面BCD于E，连接BE可得BE⊥CD，同理可得CE⊥BD，证得E是垂心，
则可得出DE⊥BC，进而可证得BC⊥面AED，即可证出BC⊥AD，故D对．
故选：D．
解：A.| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
B．由于向量的数量积是数量，且
| a |
| b |
| c |
C．由于
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
||
| a |
| a |
| b |
D．即为在四面体ABCD中，若AB⊥CD，AC⊥BD，则AD⊥BC．
如图作AE⊥面BCD于E，连接BE可得BE⊥CD，同理可得CE⊥BD，证得E是垂心，
则可得出DE⊥BC，进而可证得BC⊥面AED，即可证出BC⊥AD，故D对．
故选：D．
点评：本题考查平面向量的数量积的定义和几何意义，向量垂直的条件和向量不共线的充要条件，属于中档题．
练习册系列答案
相关题目
方程x+
=0所表示的图形是（ ）
| y |
A、 |
B、 |
C、 |
D、 |
下列判断正确的是（ ）
| A、2.71.5＞2.71.63 | ||
| B、0.782＜0.783 | ||
C、π2＜π
| ||
| D、0.9π＜0.93 |
若函数f（x）=2sin（ωx+θ）对任意x都有f（
+x）=f（
-x），则f（
）=（ ）
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| A、2或0 | B、-2或2 |
| C、0 | D、-2或0 |