题目内容
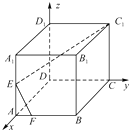 在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1棱长为2,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则点F的坐标为( )
在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1棱长为2,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则点F的坐标为( )A、(2,
| ||
B、(2,
| ||
C、(2,
| ||
D、(2,
|
考点:空间中的点的坐标
专题:空间向量及应用
分析:求出对应点的坐标,利用∠C1EF=90°转化为向量垂直关系即可.
解答:
解:由题意得E(2,0,1),C1(0,2,2),设F(2,y,0),
则
=(-2,2,1),
=(0,y,-1),
∵∠C1EF=90°,
∴
•
=2y-1=0,解得y=
,
则点F的坐标为(2,
,0),
故选:A
则
| EC1 |
| EF |
∵∠C1EF=90°,
∴
| EC1 |
| EF |
| 1 |
| 2 |
则点F的坐标为(2,
| 1 |
| 2 |
故选:A
点评:本题主要考查空间向量的应用,根据直线垂直转化为
•
=0是解决本题的关键.
| EC1 |
| EF |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)的图象是连续不断的一条曲线,且满足 f(1)>0,f(5)<0,若 f(3)>0.则f(x)在下列区间内必有零点的是( )
| A、(1,3) |
| B、(3,5) |
| C、(2,4) |
| D、(3,4) |
已知y=f(x)+x2是奇函数,且f(1)=1,若g(x)=f(x)-x2,则g(-1)=( )
| A、-4 | B、-3 | C、-1 | D、0 |
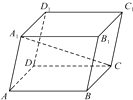 如图所示,在平行六面体ABCD-A1B1C1D1中,若
如图所示,在平行六面体ABCD-A1B1C1D1中,若| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| A1C |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|




