题目内容
函数y=tan3x的最小正周期为 ．
考点：三角函数的周期性及其求法
专题：计算题
分析：由条件利用函数y=Atan（ωx+φ）的周期为
，可得结论．
| π |
| ω |
解答：
解：函数y=tan3x的最小正周期为T=
=
．
故答案为：
．
| π |
| ω |
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题主要考查函数y=Atan（ωx+φ）的周期性，利用了函数y=Atan（ωx+φ）的周期为
，属于基础题．
| π |
| ω |
练习册系列答案
津桥教育计算小状元系列答案
相关题目
已知函数y=f（x）图象上每个点的纵坐标保持不变，将横坐标伸长到原来的2倍，然后将整个图象沿x轴向左平移
个单位，得到的图象与y=
sinx的图象相同，则y=f（x）的函数表达式为（ ）
| π |
| 2 |
| 1 |
| 2 |
A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
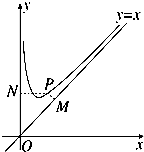如图，函数f（x）=x+