题目内容
8.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=45°,C点的仰角∠CAB=60°以及∠MAC=75°;从C点测得∠MCA=45°.已知山高BC=100m,则山高MN=$\frac{200}{3}$m.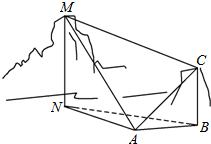
分析 由题意,通过解△ABC可先求出AC的值,解△AMC,由正弦定理可求AM的值,在RT△MNA中,AM=$\frac{200\sqrt{2}}{3}$m,∠MAN=45°,从而可求得MN的值.
解答 解:在RT△ABC中,∠CAB=60°,BC=100m,所以AC=$\frac{200}{\sqrt{3}}$m.
在△AMC中,∠MAC=75°,∠MCA=45°,从而∠AMC=60°,
由正弦定理得,$\frac{AC}{sin60°}=\frac{AM}{sin45°}$,因此AM=$\frac{200\sqrt{2}}{3}$m.
在RT△MNA中,AM=$\frac{200\sqrt{2}}{3}$m,∠MAN=45°,得MN=$\frac{200}{3}$m;
故答案为:$\frac{200}{3}$.
点评 本题主要考查了正弦定理的应用,考查了解三角形的实际应用,属于中档题.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的表面积是( )
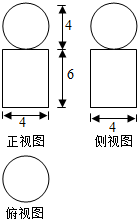

| A. | 44π | B. | 48π | C. | $\frac{116π}{3}$ | D. | $\frac{128π}{3}$ |
20.不等式|2x-1|≤7的解集是( )
| A. | {x|x≥-3} | B. | {x|x≤4} | C. | {x|-3≤x≤4} | D. | {x|x≤-3或x≥4} |