题目内容
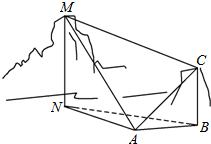
16.长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2$\sqrt{6}$,则AC1与BD所成角的余弦值为$\frac{1}{5}$.分析 连结AC、BD,交于点O,则O是AC的中点,取CC1的中点O,连结OP,由三角形中位线定理得OP∥AC1,从而∠BOP是AC1与BD所成角(或所成角的补角),由此利用余弦能求出AC1与BD所成角的余弦值.
解答  解:连结AC、BD,交于点O,则O是AC的中点,取CC1的中点O,连结OP,
解:连结AC、BD,交于点O,则O是AC的中点,取CC1的中点O,连结OP,
由三角形中位线定理得OP∥AC1,
∴∠BOP是AC1与BD所成角(或所成角的补角),
∵长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2$\sqrt{6}$,
∴OB=OC=$\frac{1}{2}\sqrt{16+9}$=$\frac{5}{2}$,PC=$\sqrt{6}$,OP=$\sqrt{6+\frac{25}{4}}$=$\frac{7}{2}$,
BP=$\sqrt{9+6}$=$\sqrt{15}$,
∴cos∠BOP=$\frac{O{B}^{2}+O{P}^{2}-B{P}^{2}}{2×OB×OP}$=$\frac{\frac{25}{4}+\frac{49}{4}-15}{2×\frac{5}{2}×\frac{7}{2}}$=$\frac{1}{5}$.
∴AC1与BD所成角的余弦值为$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
4.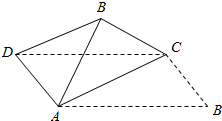 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
11.设函数y=$\frac{x+3}{x-4}$和y=$\frac{(x-3)(x+3)}{{x}^{2}-7x+12}$的值域分别为A和B,则( )
| A. | A=B | B. | A?B | C. | A?B | D. | A∪B=R |