题目内容

3．某几何体的三视图如图所示，则该几何体的表面积是（　　）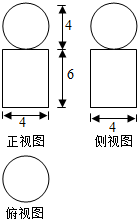
A．44πB．48πC．$\frac{116π}{3}$D．$\frac{128π}{3}$

分析 根据几何体的三视图，得出该几何体是球与圆柱体的组合体；结合图中数据求出它的表面积即可．

解答 解：根据几何体的三视图，得；
该几何体是上部为球，下部为圆柱体的组合体；
且球的直径为4，圆柱体的底面圆直径也为4，高为6；
所以该几何体的表面积为
S=4π•22+（2π•22+2π•2•6）=48π．
故选：B．

点评 本题考查了空间几何体三视图的应用问题，解题的根据是由三视图得出原图形的结构特征，是基础题目．

练习册系列答案
相关题目
13．已知函数$f（x）=\left\{\begin{array}{l}{a^x}（x＜0）\\（a-3）x+4a（x≥0）\end{array}\right.$满足对任意x1≠x2，都有（x1-x2）[f（x1）-f（x2）]＜0成立，则a的取值范围为（0，1]．
14．若方程x2+y2-2ax-4y+5a=0表示圆，则a的取值范围是a＞4或a＜1．
11．设函数y=$\frac{x+3}{x-4}$和y=$\frac{（x-3）（x+3）}{{x}^{2}-7x+12}$的值域分别为A和B，则（　　）
A．A=BB．A?BC．A?BD．A∪B=R
18．△ABC的内角A、B、C所对边的长分别为a、b、c，BC边上的高为AD．
（Ⅰ）若|$\overrightarrow{AD}$|=1，求$\overrightarrow{AB}•\overrightarrow{AD}$的值；
（Ⅱ）若b=c，$\overrightarrow{AB}•\overrightarrow{AD}$=m$\overrightarrow{AB}•\overrightarrow{AC}$，当$\frac{a}{b}$∈（$\sqrt{3}$，2）时，求实数m的取值范围．
8．如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=45°，C点的仰角∠CAB=60°以及∠MAC=75°；从C点测得∠MCA=45°．已知山高BC=100m，则山高MN=$\frac{200}{3}$m．
15．如图，圆柱高为2，底面半径为1，则在圆柱侧面上从A出发经过母线BB1到达A1的最短距离为2$\sqrt{{π}^{2}+1}$．
12．已知A、B、C是△ABC的三个内角，向量$\overrightarrow{m}$=（-1，$\sqrt{3}$），$\overrightarrow{n}$=（cosA，sinA），且$\overrightarrow{m}$•$\overrightarrow{n}$=1．
（1）求角A；
（2）若$\overrightarrow{p}$=（sinB，-3cosB），$\overrightarrow{q}$=（sinB，cosB），且$\overrightarrow{p}$⊥$\overrightarrow{q}$，求tanC．
13．已知函数f（x）=x2+|x-a|+1，a∈R
（1）试判断函数f（x）的奇偶性；
（2）若-$\frac{1}{2}$$≤a≤\frac{1}{2}$，求函数f（x）的最小值；
（3）求函数f（x）在区间[a，a+2]上的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网