题目内容
18.已知向量$\overrightarrow a=(1,2),|\overrightarrow b|=1$,且$\overrightarrow a$与$\overrightarrow b$的夹角为60°.(1)求与$\overrightarrow a$垂直的单位向量的坐标;
(2)求向量$\overrightarrow b-2\overrightarrow a$在$\overrightarrow a$上的投影.
分析 (1)设与$\overrightarrow a$垂直的单位向量的坐标为(x,y),利用单位向量与$\overrightarrow{a}$垂直得到方程组解之;
(2)根据投影的定义得到所求.
解答 解:(1)设与$\overrightarrow a$垂直的单位向量的坐标为(x,y),
则$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{x+2y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{-2\sqrt{5}}{5}}\\{y=\frac{\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{2\sqrt{5}}{5}}\\{y=-\frac{\sqrt{5}}{5}}\end{array}\right.$,
所以与$\overrightarrow a$垂直的单位向量的坐标为($-\frac{2\sqrt{5}}{5},\frac{\sqrt{5}}{5}$),或($\frac{2\sqrt{5}}{5},-\frac{\sqrt{5}}{5}$);
(2))$(\overrightarrow{b}-2\overrightarrow{a})•\overrightarrow{a}$=$\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{a}}^{2}$=$\frac{\sqrt{5}}{2}-2×5$,
所以向量$\overrightarrow b-2\overrightarrow a$在$\overrightarrow a$上的投影为$\frac{(\overrightarrow{b}-2\overrightarrow{a})•\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{\frac{\sqrt{5}}{2}-10}{\sqrt{5}}=\frac{1}{2}-2\sqrt{5}$.
点评 本题考查了平面向量的运算;熟练掌握向量的数量积公式以及几何意义是解答的关键.

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案| A. | 8+2△t | B. | 4+2+△t | C. | 7+2+△t | D. | -8+2+△t |
| A. | sin20°<cos40°<tan50° | B. | cos40°<sin20°<tan50° | ||
| C. | tan50°<cos40°<sin20° | D. | sin20°<tan50°<cos40° |
| A. | 向左平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{6}$个长度单位 | ||
| C. | 向左平移$\frac{π}{12}$个长度单位 | D. | 向右平移$\frac{π}{12}$个长度单位 |
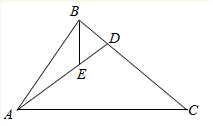 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,点D为边BC上一点,满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$,点E是AD上一点,满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$,则|$\overrightarrow{BE}$|=$\frac{2\sqrt{19}}{9}$.