题目内容

9．质点M的运动方程S=2t2-2为 则在时间段[2，2+△t]内的平均速度为（　　）
A．8+2△tB．4+2+△tC．7+2+△tD．-8+2+△t

分析 求出在时间段[2，2+△t]内的位移的增量，根据平均速度的求解公式平均速度=位移÷时间，建立等式关系即可．

解答 解：由题意△S=2（2+△t）2-2-（2×22-2）=8△t+2（△t）2，
∴在时间段[2，2+△t]内的平均速度为8+2△t，
故选A．

点评 本题主要考查了导数的运算及其几何意义，属于基础题，考查利用数学知识分析问题、解决问题的能力．

练习册系列答案
相关题目
19．已知x1＞0，x1≠1且xn+1=$\frac{{{x_n}（x_n^2+3）}}{3x_n^2+1}$（n=1，2，…）．试证：“在数列{xn}中，对任意正整数n都满足xn＜xn+1”，当此题用反证法证明，否定结论时，应为（　　）
A．对任意的正整数n，有xn=xn+1B．存在正整数n，使xn=xn+1
C．存在正整数n，使xn≥xn+1D．存在正整数n，使xn-xn-1≥0
20．已知函数f（x）=x2-ax（a≠0），g（x）=lnx，f（x）图象与x轴交于点M（M异于原点），f（x）在M处的切线为l1，g（x-1）图象与x轴交于点N且在该点处的切线为l2，并且l1与l2平行．
（Ⅰ）求f（2）的值；
（Ⅱ）已知实数t∈R，求函数y=f[xg（x）+t]，x∈[1，e]的最小值．
17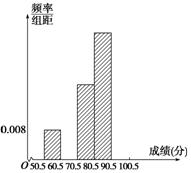．为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩进行统计．请你根据尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示），解答下列问题：
分组频数频率
50.5～60.540.08
60.5～70.50.16
70.5～80.510
80.5～90.5160.32
90.5～100.5
合计50
（1）填充频率分布表中的空格；
（2）补全频率分布直方图；
（3）若成绩在80.5～90.5分的学生可以获得二等奖，问获得二等奖的学生约为多少人？
4．已知函数f（x）=x-lnx，g（x）=x3+x2f（x）-16x+20．
（Ⅰ）求f（x）的单调区间及极值；
（Ⅱ）求证：g（x）的图象恒在x轴的上方．
14．一辆卡车宽2.7米，要经过一个半径为4.5米的半圆形隧道（双车道，不得违章），则这辆卡车的平顶车篷篷顶距离地面的高度不得超过（　　）米．
A．1.4B．3.0C．3.6D．4.5
1．已知等差数列{an}的前n项和为Sn，首项为1的等比数列{bn}的公比为q，S2=a3=b3，且a1，a3，b4成等比数列．
（1）求{an}和{bn}的通项公式；
（2）设${c_n}=k+{a_n}+{log_3}{b_n}（k∈N_{\;}^+），若\frac{1}{c_1}，\frac{1}{c_2}，\frac{1}{c_t}$（t≥3）成等差数列，求k和t的值．
18．已知向量$\overrightarrow a=（1，2），|\overrightarrow b|=1$，且$\overrightarrow a$与$\overrightarrow b$的夹角为60°．
（1）求与$\overrightarrow a$垂直的单位向量的坐标；
（2）求向量$\overrightarrow b-2\overrightarrow a$在$\overrightarrow a$上的投影．
4．在等差数列{an}中，a3+3a8+a13=120，则a8=（　　）
A．24B．22C．20D．25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网