题目内容
7.为得到函数y=sin(2x+$\frac{π}{6}$)的图象,只需将函数y=sin2x的图象( )| A. | 向左平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{6}$个长度单位 | ||
| C. | 向左平移$\frac{π}{12}$个长度单位 | D. | 向右平移$\frac{π}{12}$个长度单位 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:根据将函数y=sin2x的图象向左平移$\frac{π}{12}$个长度单位,可得函数y=sin(2x+$\frac{π}{6}$)的图象,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
17.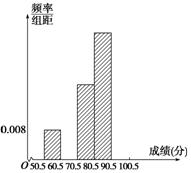 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),A,B为双曲线的左右顶点,若点M在双曲线上,且满足△ABM为一个顶角为120°的等腰三角形,则双曲线的渐近线方程是( )
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±2x | D. | y=±$\frac{\sqrt{2}}{2}$x |
4.在等差数列{an}中,a3+3a8+a13=120,则a8=( )
| A. | 24 | B. | 22 | C. | 20 | D. | 25 |
1.设F1和F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,若△F1PF2的面积是2,则b的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
2.为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如图的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2>k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
| A. | 95% | B. | 99% | C. | 99.5% | D. | 99.9% |