题目内容
设数列 的前
的前 项和为
项和为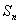 ,
, ,且对任意正整数
,且对任意正整数 ,点
,点 在
在 直线上.
直线上.
(1)求数列 的通项公式;
的通项公式;
(2)是否存在实数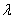 ,使得数列
,使得数列 为等差数列?若存在,求出
为等差数列?若存在,求出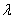 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
解析:(1) 点
点 都在函数
都在函数 的图像上,
的图像上,
 ,
,
当 时,
时,
当 时,
时, 满足上式,所以数列
满足上式,所以数列 的通项公式为
的通项公式为
(2)由 求导可得
求导可得
 过点
过点 的切线的斜率为
的切线的斜率为 ,
, .
.
 .
.
 ①
①
由①×4,得
 ②
②
①-②得:


 .
.
(3) ,
, .
.
又 ,其中
,其中 是
是 中的最小数,
中的最小数,
 是公差是4的倍数,
是公差是4的倍数,
又 ,
, ,解得m=27.
,解得m=27.
所以 ,设等差数列的公差为
,设等差数列的公差为 ,则
,则
 ,所以
,所以 的通项公式为
的通项公式为 .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 满足
满足 ,则下列关系式恒成立的是( )
,则下列关系式恒成立的是( ) B.
B.  C.
C.  D.
D. 
 的首项
的首项 为
为 ,
, 为等差数列且
为等差数列且 .若则
.若则 ,
, ,则
,则 ( )
( ) C.8 D.11
C.8 D.11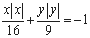 的曲线即为函数
的曲线即为函数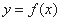 的图像,对于函数
的图像,对于函数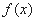 在R上单调递减;②函数
在R上单调递减;②函数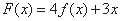 不存在零点;③函数
不存在零点;③函数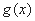 和
和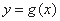 的图像就是方程
的图像就是方程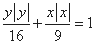 确定的曲线.其中所有正确的命题序号是 ( )
确定的曲线.其中所有正确的命题序号是 ( ) -
- =1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点
=1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点 ,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
 的定义域为 ( )
的定义域为 ( ) B.
B.  C.
C.  D.
D. 
