题目内容
已知向量a＝(m，cos 2x)，b＝(sin 2x，n)，函数f(x)＝a·b，且y＝f(x)的图像过点
(1)求m，n的值；
(2)将y＝f(x)的图像向左平移φ(0＜φ＜π)个单位后得到函数y＝g(x)的图像，若y＝g(x)图像上各最高点到点(0，3)的距离的最小值为1，求y＝g(x)的单调递增区间．
解：(1)由题意知，f(x)＝a·b＝msin 2x＋ncos 2x.
即
解得m＝
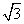，n＝1.
练习册系列答案
相关题目
的前
项和为
，
，且对任意正整数
在
直线上.
，使得数列
为等差数列？若存在，求出
．
时，求
在区间
上的最值；
时，有
恒成立，求
的取值范围．
为
的最小正周期，
，且
．求
的值．
的图像向右平移
个单位长度，所得图像对应的函数( )
上单调递减
上单调递增
上单调递减
的图像关于直线x＝
对称，且图像上相邻两个最高点的距离为π.
的值．
则( )
B．3α＋β＝
，则△ABC的面积是( )
C.
D．3 
题目内容
已知向量a＝(m，cos 2x)，b＝(sin 2x，n)，函数f(x)＝a·b，且y＝f(x)的图像过点
(1)求m，n的值；
(2)将y＝f(x)的图像向左平移φ(0＜φ＜π)个单位后得到函数y＝g(x)的图像，若y＝g(x)图像上各最高点到点(0，3)的距离的最小值为1，求y＝g(x)的单调递增区间．
解：(1)由题意知，f(x)＝a·b＝msin 2x＋ncos 2x.
即
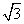解得m＝，n＝1.