题目内容
向量 =(x,y),
=(x,y), =(x2,y2),
=(x2,y2), =(1,1)
=(1,1) =(
=(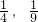 ),若
),若 •
• =1,
=1, •
• =1,则这样的
=1,则这样的
- A.只有一个
- B.多于2个
- C.只有2个
- D.不存在
C
分析:由 =1,
=1, 可知,要判断满足条件的
可知,要判断满足条件的 的个数,只要判断
的个数,只要判断 的根的个数即可.
的根的个数即可.
解答:∵ =1,
=1,
而 可得13x2-8x-32=0
可得13x2-8x-32=0
则方程有2个不相等的实根
即 有两个
有两个
故选C.
点评:本题以向量的数量积的坐标表示为切入点,主要考查了直线与椭圆的相交关系的应用,解题的关键是把所求的问题转化为判断二次方程的根的个数.
分析:由
 =1,
=1, 可知,要判断满足条件的
可知,要判断满足条件的 的个数,只要判断
的个数,只要判断 的根的个数即可.
的根的个数即可.解答:∵
 =1,
=1,
而
 可得13x2-8x-32=0
可得13x2-8x-32=0则方程有2个不相等的实根
即
 有两个
有两个故选C.
点评:本题以向量的数量积的坐标表示为切入点,主要考查了直线与椭圆的相交关系的应用,解题的关键是把所求的问题转化为判断二次方程的根的个数.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知向量a=(x,y),向量b∥a,|b|=|a|,且b≠a,则b的坐标为( )
| A、(x,-y) | B、(-x,-y) | C、(-y,-x) | D、(-x,y) |
若空间三点A(0,1,5),B(1,5,0),C(5,0,1),向量
=(x,y,z)与
,
分别垂直,且|
|=
,则x2y2z2的值是( )
. |
| a |
| AB |
| AC |
. |
| a |
| 15 |
| A、215 | B、152 |
| C、125 | D、521 |