题目内容
设椭圆E:
+
=1(a,b>0),短轴长为4,离心率为
,O为坐标原点,
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
⊥
?若存在,求出该圆的方程,若不存在说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由椭圆E的短轴长为4,离心率为
,可得2b=4,e=
=
,又a2=b2+c2.解出即可.
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
⊥
,设该圆的切线方程为y=kx+m,与椭圆方程联立可得(1+2k2)x2+4kmx+2m2-8=0,△>0,化为8k2-m2+4>0,可得根与系数的关系,
⊥
?x1x2+y1y2=0,可得3m2-8k2-8=0,由于直线y=kx+m为圆心在原点的圆的一条切线,可得x2+y2=
,此时圆的切线y=kx+m都满足m≥
或m≤-
,而当切线的斜率不存在时,也成立.
| ||
| 2 |
| ||
| 2 |
| c |
| a |
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
| OA |
| OB |
| OA |
| OB |
| 8 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
解答:
解:(1)∵椭圆E:
+
=1(a,b>0),短轴长为4,离心率为
,
∴2b=4,e=
=
,又a2=b2+c2.
解得
,
∴椭圆E的方程为
+
=1.
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
⊥
,
设该圆的切线方程为y=kx+m,
联立
化为(1+2k2)x2+4kmx+2m2-8=0,
则△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,化为8k2-m2+4>0,
∴x1+x2=-
,x1x2=
,
y1y2=(k1x+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
-
+m2=
.
∵
⊥
,
∴x1x2+y1y2=0,
∴
+
=0,
∴3m2-8k2-8=0,
∴k2=
≥0,
又8k2-m2+4>0,
∴
,∴m2≥
,即m≥
或m≤-
,
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴圆的半径为r=
,r2=
=
=
,r=
,
所求的圆为x2+y2=
,
此时圆的切线y=kx+m都满足m≥
或m≤-
,
而当切线的斜率不存在时,切线为x=±
与椭圆
+
=1的两个交点为(
,±
)或(-
,±
)满足
⊥
.
综上,存在圆心在原点的圆x2+y2=
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
⊥
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴2b=4,e=
| ||
| 2 |
| c |
| a |
解得
|
∴椭圆E的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
| OA |
| OB |
设该圆的切线方程为y=kx+m,
联立
|
则△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,化为8k2-m2+4>0,
∴x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
y1y2=(k1x+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
| k2(2m2-8) |
| 1+2k2 |
| 4k2m2 |
| 1+2k2 |
| m2-8k2 |
| 1+2k2 |
∵
| OA |
| OB |
∴x1x2+y1y2=0,
∴
| 2m2-8 |
| 1+2k2 |
| m2-8k2 |
| 1+2k2 |
∴3m2-8k2-8=0,
∴k2=
| 3m2-8 |
| 8 |
又8k2-m2+4>0,
∴
|
| 8 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∵直线y=kx+m为圆心在原点的圆的一条切线,
∴圆的半径为r=
| |m| | ||
|
| m2 |
| 1+k2 |
| m2 | ||
1+
|
| 8 |
| 3 |
2
| ||
| 3 |
所求的圆为x2+y2=
| 8 |
| 3 |
此时圆的切线y=kx+m都满足m≥
2
| ||
| 3 |
2
| ||
| 3 |
而当切线的斜率不存在时,切线为x=±
2
| ||
| 3 |
| x2 |
| 8 |
| y2 |
| 4 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| OA |
| OB |
综上,存在圆心在原点的圆x2+y2=
| 8 |
| 3 |
| OA |
| OB |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相切相交问题转化为方程联立可得△≥0及根与系数的关系、向量垂直与数量积的关系、点到直线的距离公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
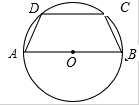 四边形ABCD是⊙O的内接等腰梯形,AB为直径,且AB=4.设∠BOC=θ,ABCD的周长为L.
四边形ABCD是⊙O的内接等腰梯形,AB为直径,且AB=4.设∠BOC=θ,ABCD的周长为L.