Question

6．如图，在四棱椎P-ABCD中，底面ABCD为矩形，平面PCD⊥面ABCD，BC=1，AB=2，PC=$PD=\sqrt{2}$，E为PA中点．
（1）求证：PC∥平面BED；
（2）求三棱锥E-PBD的体积．

Answer 1

分析 （1）设AC与BD的交点为F，连结EF，推导出EF∥PC，由此能证明PC∥平面BED．
（2）取CD中点O，连接PO，PO⊥CD，则PO⊥平面ABCD．连接AO，取AO中点K，则$EK∥\frac{1}{2}PO=\frac{1}{2}$，且EK⊥平面ABCD，由此能出三棱锥E-PBD的体积．

解答 证明：（1）设AC与BD的交点为F，连结EF．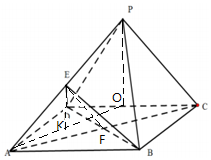
∵ABCD为矩形，所以F为AC的中点．
在△PAC中，由已知E为PA中点，
∴EF∥PC．
又EF?平面BED，PC?平面BED，
∴PC∥平面BED．
解：（2）取CD中点O，连接PO，PO⊥CD，平面PCD⊥平面ABCD，
∴PO⊥平面ABCD．
连接AO，取AO中点K，则$EK∥\frac{1}{2}PO=\frac{1}{2}$，且EK⊥平面ABCD．
∴三棱锥E-PBD的体积：
${V_{E-PBD}}={V_{P-ABCD}}-{V_{P-BCD}}=\frac{1}{3}×2×1×1-$$\frac{1}{3}×\frac{1}{2}×2×1×\frac{1}{2}-\frac{1}{3}×\frac{1}{2}×2×1×1=\frac{1}{6}$．

点评 本题考查几何体的体积的求法，考查线面平行的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．