题目内容
10．已知直线l：x+y-4=0，定点P（2，0），E，F分别是直线l和y轴上的动点，则△PEF的周长的最小值为（ ）| A． | 2$\sqrt{10}$ | B． | 6 | C． | 3$\sqrt{3}$ | D． | 2$\sqrt{5}$ |
分析 求得点P（2，0）关于直线l：x+y-4=0的对称点P′的坐标，再求得P′关于y轴的对称点为P″的坐标，可得此时△PEF的周长的最小值为PP″，计算求得结果．
解答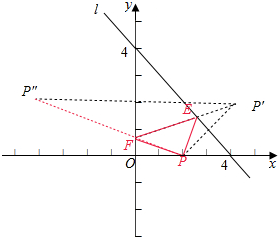 
解：如图所示：设P′是点P（2，0）关于直线l：x+y-4=0的对称点，设P′（a，b），
则由$\left\{\begin{array}{l}{\frac{b-0}{a-2}=-1}\\{\frac{a+2}{2}+\frac{b+0}{2}-4=0}\end{array}\right.$求得$\left\{\begin{array}{l}{a=4}\\{b=2}\end{array}\right.$，可得P′（4，2）．
设P′关于y轴的对称点为P″（m，n），易得P″（-4，2），则直线PP″和y轴的交点为F，
FP′和直线l的交点为E，则此时，
△PEF的周长为EF+EP+PF=EF+EP′+PF=P′F+PF=P″F+PF=PP″=2$\sqrt{10}$，
为最小值，
故选：A．
点评 本题主要考查求点关于直线的对称点的坐标，线段的中垂线的性质，三点共线的性质，属于中档题．
练习册系列答案
应用题作业本系列答案
相关题目
18．投掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币数字一面向上”为事件A，“骰子向上的点数是偶数”为事件B，则事件A，B中至少有一件发生的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{12}$ |
5．已知直线$\sqrt{2}$ax+by=1（其中a，b为非零实数），与圆x+y2=1相交于A，B两点，O为坐标原点，且△AOB为直角三角形，则$\frac{1}{{a}^{2}}$+$\frac{2}{{b}^{2}}$的最小值为（ ）
| A． | 4 | B． | 2$\sqrt{2}$ | C． | 5 | D． | 8 |
15．
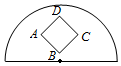如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）
如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）| A． | $\frac{1}{π}$ | B． | $\frac{1}{2π}$ | C． | $\frac{2}{π}$ | D． | $\frac{π}{4}$ |
2．已知二项式（3-x）n（n∈N*）展开式中所有项的系数之和为a，所有项的系数的绝对值之和为b，则$\frac{b}{a}$+$\frac{a}{b}$的最小值为（ ）
| A． | $\frac{9}{2}$ | B． | 2 | C． | $\frac{13}{6}$ | D． | $\frac{5}{2}$ |
19．函数f（x）=sin（ωx+φ）（其中|φ|＜$\frac{π}{2}$）的图象如图所示，则f（2016π）=（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
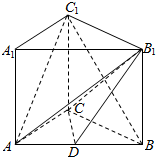如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AC=4，BC=3，AB=5，AA1=4，点D是AB的中点．