题目内容

15．给出下列四个命题：①没有公共点的两条直线平行；②互相垂直的两条直线是相交直线；③既不平行也不相交的两条直线是异面直线；④不同在任何一个平面内的两条直线是异面直线．
其中正确的命题是（　　）
A．①②B．②③C．①④D．③④

分析 在①中，两直线有可能异面；在②中，两直线有可能异面垂直；由异面直线的定义得③④正确．

解答 解：在①中，没有公共点的两条直线平行或异面，故①错误；
在②中，互相垂直的两条直线有可能相交且垂直，有可能异面垂直，
故互相垂直的两条直线也有可能是异面直线，故②错误；
在③中，由异面直线的定义得既不平行也不相交的两条直线是异面直线，故③正确；
在④中，由异面直线的定义得不同在任何一个平面内的两条直线是异面直线，故④正确．
故选：D．

点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．

练习册系列答案
相关题目
5．已知直线$\sqrt{2}$ax+by=1（其中a，b为非零实数），与圆x+y2=1相交于A，B两点，O为坐标原点，且△AOB为直角三角形，则$\frac{1}{{a}^{2}}$+$\frac{2}{{b}^{2}}$的最小值为（　　）
A．4B．2$\sqrt{2}$C．5D．8
6．已知函数f（x）=2sinωx，其中常数ω＞0．
（Ⅰ）若y=f（x）在[-$\frac{π}{4}$，$\frac{2π}{3}$]上单调递增，求ω的取值范围；
（Ⅱ）令ω=2，将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位，再向上平移1个单位，得到函数y=g（x）的图象求y=g（x）的图象离原点O最近的对称中心．
3．已知数列{an}的前n项和为Sn=2n-3n，则a6+a7+a8=215．
10．已知p：“方程$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{3}$=1”表示双曲线；q：“关于x的方程x2-mx+1=0没有实数根”．
若“￢p”和“p∨q”都是真命题，求m的取值范围．
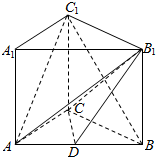20．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AC=4，BC=3，AB=5，AA1=4，点D是AB的中点．
（1）求证：AC1∥平面CDB1；
（2）求直线AB1与平面BB1C1C所成角的正切值．
7．已知抛物线E：y=mx2（m＞0），圆C：x2+（y-2）2=4，点F是抛物线E的焦点，点N（x0，y0）（x0＞0，y0＞0）为抛物线E上的动点，点M（2，-$\frac{1}{2}$），线段MF恰被抛物线E平分．
（1）求m的值；
（2）若y0＞4，过点N向圆C作切线，求两条切线与x轴围成的三角形面积的最小值．
4．函数y=$\sqrt{lo{g}_{2}（2x-1）}$的定义域是（　　）
A．（$\frac{1}{2}$，1）B．（$\frac{1}{2}$，1]C．（$\frac{1}{2}$，+∞）D．[1，+∞）
5．设α是第二象限角，P（x，4）为其终边上的一点，且cosα=$\frac{x}{5}$，则tan2α=$\frac{24}{7}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网