题目内容
若sinθ=-
,cosθ=-
,则角θ的终边一定落在下列射线上的是( )
| 24 |
| 25 |
| 7 |
| 25 |
| A、7x-24y=0(x>0) |
| B、24x-7y=0(x<0) |
| C、7x-24y=0(x<0) |
| D、24x-7y=0(x>0) |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由sinθ=-
<0,cosθ=-
<0,可得θ的终边落在第三象限,且角θ的终边所在直线的斜率k=
=
,
即可得出.
| 24 |
| 25 |
| 7 |
| 25 |
| sinθ |
| cosθ |
| 24 |
| 7 |
即可得出.
解答:
解:∵sinθ=-
<0,cosθ=-
<0,
∴θ的终边落在第三象限,
且角θ的终边所在直线的斜率k=
=
,
∴角θ的终边一定落在下列射线上的是24x-7y=0(x<0).
故选:B.
| 24 |
| 25 |
| 7 |
| 25 |
∴θ的终边落在第三象限,
且角θ的终边所在直线的斜率k=
| sinθ |
| cosθ |
| 24 |
| 7 |
∴角θ的终边一定落在下列射线上的是24x-7y=0(x<0).
故选:B.
点评:本题考查了直线的倾斜角与斜率,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α是第三象限角,则
-
=( )
| |sinα| |
| sinα |
| cosα |
| |cosα| |
| A、0 | B、1 | C、2 | D、-2 |
设数列{an}是等差数列,其前n项和为Sn,若a6=2,S5=30,则S8=( )
| A、31 | B、32 | C、33 | D、34 |
设正项等差数列{an}的前n项和为Sn,若S2012=2012,则
+
的最小值为( )
| 1 |
| a1 |
| 1 |
| a2012 |
| A、1 | B、2 | C、4 | D、8 |
对于任意实数a、b、c、d,下列命题:
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
<
中.
真命题个数为( )
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
| 1 |
| a |
| 1 |
| b |
真命题个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
对于原命题:“单调函数不是周期函数”,下列陈述正确的是 ( )
| A、逆命题为“周期函数不是单调函数” |
| B、否命题为“单调函数是周期函数” |
| C、逆否命题为“周期函数是单调函数” |
| D、以上三者都不正确 |
 如图,已知在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m至点C处,测得顶端A的仰角为2θ,再继续前进10
如图,已知在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m至点C处,测得顶端A的仰角为2θ,再继续前进10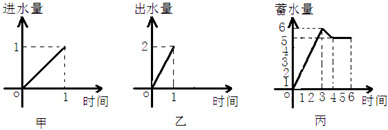 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断: