题目内容
已知函数f(x)=x2+
,(x≠0,a∈R)
(1)讨论f(x)的奇偶性,并说明理由;
(2)已知a=16,用定义法证明f(x)在[2,+∞)是单调递增的.
| a |
| x |
(1)讨论f(x)的奇偶性,并说明理由;
(2)已知a=16,用定义法证明f(x)在[2,+∞)是单调递增的.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,分类讨论,函数的性质及应用
分析:(1)讨论当a=0时,当a≠0时,运用函数的奇偶性的定义,即可判断;
(2)运用函数的单调性的定义证明,注意作差、变形和定符号、下结论几个步骤.
(2)运用函数的单调性的定义证明,注意作差、变形和定符号、下结论几个步骤.
解答:
(1)解:当a=0时,f(x)=x2,此时f(x)为偶函数;
当a≠0时,f(-x)=(-x)2+
=x2-
f(-x)≠f(x),且f(-x)≠-f(x),
则f(x)不为奇函数也不是偶函数;
(2)证明:由a=16,得f(x)=x2+
.
取任意的m,n∈[2,+∞),且m<n,f(m)-f(n)=m2+
-n2-
=(m-n)(m+n)+
=(m-n)[(m+n)-
],
由于2≤m<n,则m-n<0,m+n>4,mn>4,则
<4,m+n-
>0,
故f(m)-f(n)<0,也即f(m)<f(n),
所以f(x)在[2,+∞)上是单调递增的.
当a≠0时,f(-x)=(-x)2+
| a |
| -x |
| a |
| x |
f(-x)≠f(x),且f(-x)≠-f(x),
则f(x)不为奇函数也不是偶函数;
(2)证明:由a=16,得f(x)=x2+
| 16 |
| x |
取任意的m,n∈[2,+∞),且m<n,f(m)-f(n)=m2+
| 16 |
| m |
| 16 |
| n |
=(m-n)(m+n)+
| 16(n-m) |
| mn |
| 16 |
| mn |
由于2≤m<n,则m-n<0,m+n>4,mn>4,则
| 16 |
| mn |
| 16 |
| mn |
故f(m)-f(n)<0,也即f(m)<f(n),
所以f(x)在[2,+∞)上是单调递增的.
点评:本题考查函数的奇偶性和单调性的判断,考查分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A、a2-2a-16 |
| B、a2+2a-16 |
| C、-16 |
| D、16 |
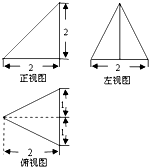
如图是某三棱锥的三视图,则这个三棱锥的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
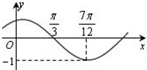 函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
下列三个图象中能表示y是x的函数图象的个数是( )


| A、0 | B、1 | C、2 | D、3 |