题目内容
14.在△ABC中,$BC=2\sqrt{2}$,AC=2,且$cos({A+B})=-\frac{{\sqrt{2}}}{2}$.(Ⅰ)求AB的长度;
(Ⅱ)若f(x)=sin(2x+C),求y=f(x)与直线$y=\frac{{\sqrt{3}}}{2}$相邻交点间的最小距离.
分析 (Ⅰ)利用诱导公式求得cosC,可得C的值,咋利用余弦定理求得AB的长度.
(Ⅱ)由f(x)=sin(2x+C),求得x1、x2的值,可得|x1-x2|的最小值.
解答 解:(Ⅰ)∵$cosC=cos[{π-({A+B})}]=-cos({A+B})=\frac{{\sqrt{2}}}{2}$,∴C=45°.
∵$BC=2\sqrt{2}$,AC=2,∴$A{B^2}=A{C^2}+B{C^2}-2AC•BCcosC={(2\sqrt{2})^2}+{2^2}-8\sqrt{2}cos{45^0}$=4,∴AB=2.
(Ⅱ)由$f(x)=sin(2x+\frac{π}{4})=\frac{{\sqrt{3}}}{2}$,解得 $2x+\frac{π}{4}=2kπ+\frac{π}{3}$或$2x+\frac{π}{4}=2kπ+\frac{2π}{3}$,k∈Z,
解得${x_1}={k_1}π+\frac{π}{24}$,或${x_2}={k_2}π+\frac{5π}{24}$,k1,k2∈Z.
因为 $|{{x_1}-{x_2}}|=|{({k_1}-{k_2})π+\frac{π}{6}}|≥\frac{π}{6}$,当k1=k2时取等号,
所以 当$f(x)=\frac{{\sqrt{3}}}{2}$时,相邻两交点间最小的距离为$\frac{π}{6}$.
点评 本题主要考查诱导公式,余弦定理,正弦函数的图象特征,属于基础题.

练习册系列答案
相关题目
4.已知i为虚数单位,若复数i•z=$\sqrt{2}$-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.在复平面内,复数g(x)满足$z({1+i})=|{1+\sqrt{3}i}|$,则z的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.已知随机变量X~N(1,σ2),若P(0<X<2)=0.4,则P(X≤0)=( )
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
9.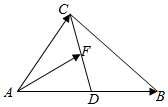 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )| A. | $6+2\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | $3+2\sqrt{2}$ |
3.已知点A(1,1),B(2,1),C(1,2),若λ∈[-1,2],μ∈[2,3],则|λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$|的取值范围是( )
| A. | [2,10] | B. | [$\sqrt{5}$,$\sqrt{13}$] | C. | [1,5] | D. | [2,$\sqrt{13}$] |
4.已知tanα=-$\frac{1}{3}$.则$\frac{1}{co{s}^{2}α}$等于( )
| A. | 9 | B. | 10 | C. | $\frac{1}{9}$ | D. | $\frac{10}{9}$ |