题目内容
4.已知tanα=-$\frac{1}{3}$.则$\frac{1}{co{s}^{2}α}$等于( )| A. | 9 | B. | 10 | C. | $\frac{1}{9}$ | D. | $\frac{10}{9}$ |
分析 由已知得cosα=-3sin2α,从而cos2α+sin2α=10sin2α=1,由此能求出结果.
解答 解:∵tanα=$\frac{sinα}{cosα}$=-$\frac{1}{3}$,∴cosα=-3sin2α,
∴cos2α+sin2α=10sin2α=1,
∴sin2α=$\frac{1}{10}$,cos2α=1-sin2α=$\frac{9}{10}$,
∴$\frac{1}{co{s}^{2}α}$=$\frac{10}{9}$.
故选:D.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意同角三角函数性质的合理运用.

练习册系列答案
相关题目
15.已知随机变量x服从正态分布N(3,σ2),且P(x≤4)=0.84,则P(2<x<4)=( )
| A. | 0.84 | B. | 0.68 | C. | 0.32 | D. | 0.16 |
9.450°<α<540°,$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}}$=-sin$\frac{α}{2}$.
16.在△ABC中,三个内角A,B,C的对边分别是a,b、c,如果a:b:c=1:1:$\sqrt{3}$,则A:B:C=( )
| A. | 1:1:2 | B. | 1:1:3 | C. | 1:1:4 | D. | 1:1:5 |
14.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
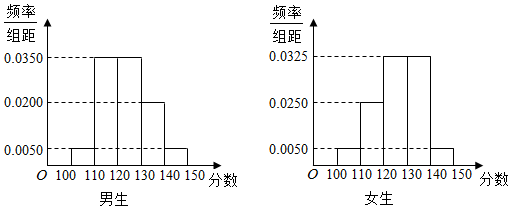
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |