题目内容
【题目】在边长为2的菱形
中，
，将菱形沿对角线
折起，使得平面
平面
，则所得三棱锥
的外接球表面积为（ ）
A.
B.
C.
D.
【答案】C
【解析】
由题意画出图形，由于
与
均为边长为2的等边三角形，取
中点
，连接
，
，则
，根据面面垂直的性质可得出
平面
，再确定
为三棱锥
的外接球的球心，结合已知求出三棱锥外接球的半径
，最后根据球的表面积公式求出外接球的表面积.
解：
在边长为2的菱形
中，
，
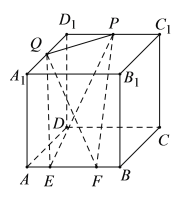
如图，
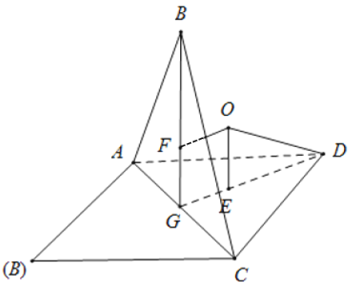
由已知可得，与均为边长为2的等边三角形，
取中点，连接，，则，
，
平面
平面，交线为，
而
平面
，则平面，
分别取
与
的外心
，
，
过，分别作两面的垂线，相交于，
则为三棱锥的外接球的球心，
由
与均为等边三角形且边长为2，
可得
，
，
，
即三棱锥外接球的半径：
，
三棱锥的外接球的表面积为：
.
故选：C.
练习册系列答案
相关题目
