题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求![]() 的参数方程与
的参数方程与![]() 的直角坐标方程;
的直角坐标方程;
(II)射线![]() 与
与![]() 交于异于极点的点
交于异于极点的点![]() ,与
,与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
【答案】(I)![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 的直角坐标方程为
的直角坐标方程为![]() ;(II)
;(II)![]() .
.
【解析】
(I)由题意,可得曲线![]() 是以(1,0)为圆心,1为半径的圆,即可求得曲线
是以(1,0)为圆心,1为半径的圆,即可求得曲线![]() 的参数方程,根据极坐标与直角坐标的互化公式,即可求得曲线
的参数方程,根据极坐标与直角坐标的互化公式,即可求得曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)由(I)得到曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将射线
,将射线![]() 代入曲线
代入曲线![]() 的方程,求得关于
的方程,求得关于![]() 的方程,根据极径的几何意义,即可求解.
的方程,根据极径的几何意义,即可求解.
(I)由![]() ,得
,得![]() .所以曲线
.所以曲线![]() 是以(1,0)为圆心,
是以(1,0)为圆心,
1为半径的圆,所以曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
由![]() ,得
,得![]() ,所以
,所以![]() ,则曲线
,则曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(II)由(I)易得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,则射线
,则射线![]() 与曲线
与曲线![]() 的交点的极径为
的交点的极径为![]() ,
,
射线![]() 与曲线
与曲线![]() 的交点的极径
的交点的极径![]() 满足
满足![]() ,
,
解得![]() .
.
所以![]() .
.

【题目】已知曲线![]() 的参数方程为
的参数方程为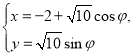 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线![]() 的极坐标方程化为直角坐标方程.
的极坐标方程化为直角坐标方程.
(2)曲线![]() ,
,![]() 是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
是否相交?若相交,请求出公共弦长;若不相交,请说明理由.
【题目】2017年9月支付宝宣布在肯德基的KPRO餐厅上线刷脸支付,也即用户可以不用手机,单单通过刷脸就可以完成支付宝支付,这也是刷脸支付在全球范围内的首次商用试点.某市随机抽查了每月用支付宝消费金额不超过3000元的男女顾客各300人,调查了他们的支付宝使用情况,得到如下频率分布直方图:
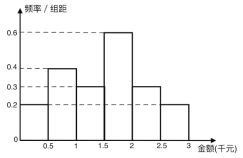
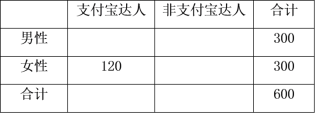
若每月利用支付宝支付金额超过2千元的顾客被称为“支付宝达人”, 利用支付宝支付金额不超过2千元的顾客称为“非支付宝达人”.
(I)若抽取的“支付宝达人”中女性占120人,请根据条件完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
(II)支付宝公司为了进一步了解这600人的支付宝使用体验情况和建议,从“非支付宝达人” “支付宝达人”中用分层抽样的方法抽取8人.若需从这8人中随机选取2人进行问卷调查,求至少有1人是“支付宝达人”的概率.
附:参考公式与参考数据如下
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |