题目内容
13.函数y=sinα•tanα的奇偶性是偶函数.分析 判断函数的定义域和f(-x)与f(x)的关系.
解答 解:∵y=sinx是奇函数,y=tanx是奇函数,
∴y=sinx•tanx是偶函数.
故答案为:偶函数.
点评 本题考查了函数奇偶性的判断,属于基础通.

练习册系列答案
相关题目
3.已知点A(1,1),B(2,1),C(1,2),若λ∈[-1,2],μ∈[2,3],则|λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$|的取值范围是( )
| A. | [2,10] | B. | [$\sqrt{5}$,$\sqrt{13}$] | C. | [1,5] | D. | [2,$\sqrt{13}$] |
4.已知tanα=-$\frac{1}{3}$.则$\frac{1}{co{s}^{2}α}$等于( )
| A. | 9 | B. | 10 | C. | $\frac{1}{9}$ | D. | $\frac{10}{9}$ |
1.下列不等式中成立的是( )
| A. | sin(-$\frac{π}{8}$)<sin(-$\frac{π}{10}$) | B. | sin(-$\frac{23}{5}π$)$>sin(-\frac{17}{4}π)$ | ||
| C. | sin3>sin2 | D. | sin$\frac{7π}{5}$>sin(-$\frac{2π}{5}$) |
8.若tanα=3,则tan(α-$\frac{π}{4}$)=( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
5.如图是一个程序框图,则输出的S的值是( )


| A. | -1 | B. | 0 | C. | 8 | D. | 9 |
3.某企业2014年2月份生产A,B,C三种产品共6000件,根据分层抽样的结果,该企业统计员制作了如下的统计表格:
由于不小心,表格中B,C产品的有关数据已被污染看不清楚,统计员记得B产品的样本容量比C产品的样本容量多20,根据以上信息,可得C产品数量是( )
| 产品分类 | A | B | C |
| 产品数量 | 2 600 | ||
| 样本容量 | 260 |
| A. | 160 | B. | 180 | C. | 1600 | D. | 1800 |
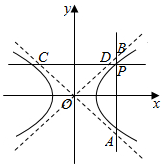 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.