题目内容
3.某企业2014年2月份生产A,B,C三种产品共6000件,根据分层抽样的结果,该企业统计员制作了如下的统计表格:| 产品分类 | A | B | C |
| 产品数量 | 2 600 | ||
| 样本容量 | 260 |
| A. | 160 | B. | 180 | C. | 1600 | D. | 1800 |
分析 根据分层抽样的定义,建立方程关系即可得到结论.
解答 解:∵$\frac{样本容量}{产品数量}$=$\frac{260}{2600}$=$\frac{1}{10}$,
∴样本的总容量是600,设C产品样本容量是x,
根据B产品的样本容量比C产品的样本容量多20,
则B产品的样本容量是x+20,
又x+x+20=600-260,即x=160,
∴可得C产品数量是160$÷\frac{1}{10}$=1600
故选:C.
点评 本题主要考查分层抽样的应用,根据条件建立方程是解决本题的关键,比较基础.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
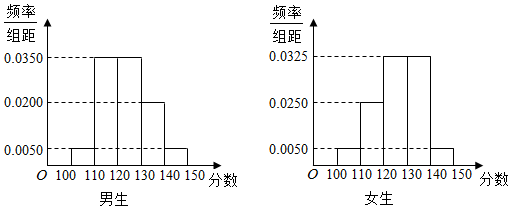
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
11.若实数x,y满足$\left\{\begin{array}{l}x+y-3≥0\\ x-y-3≤0\\ 0≤y≤1\end{array}\right.$,则$z=\frac{2x+y}{x+y}$的最小值为( )
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
18.设点P是曲线C:y=x3-$\sqrt{3}$x+$\frac{2}{3}$上的任意一点,曲线C在P点处的切线的倾斜角为α,则角α的取值范围是( )
| A. | [$\frac{2}{3}$π,π) | B. | ($\frac{π}{2}$,$\frac{5}{6}$π] | C. | [0,$\frac{π}{2}$)∪[$\frac{5}{6}$π,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{2}{3}$π,π) |
8.已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若?x∈(0,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是( )
| A. | $({-∞,2\sqrt{2}})$ | B. | $({-∞,2\sqrt{2}}]$ | C. | $({0,2\sqrt{2}}]$ | D. | $({2\sqrt{2},+∞})$ |
15.已知函数f(x)的图象在点(x0,f(x0))处的切线方程l:y=g(x),若函数f(x)满足?x∈l(其中I为函数f(x)的定义域),当x≠x0时,[f(x)-g(x)](x-x0)>0恒成立,则称x0为函数f(x)的“转折点”,若函数f(x)=lnx-ax2-x在(0,e]上存在一个“转折点”,则a的取值范围为( )
| A. | $[{\frac{1}{{2{e^2}}},+∞})$ | B. | $({-1,\frac{1}{{2{e^2}}}}]$ | C. | $[{-\frac{1}{{2{e^2}}},1})$ | D. | $({-∞,-\frac{1}{{2{e^2}}}}]$ |