题目内容
15.求证:2(1+cosα)-sin2α=4cos4$\frac{α}{2}$.分析 利用1+cosα=$2co{s}^{2}\frac{α}{2}$及同角三角函数关系式能证明2(1+cosα)-sin2α=4cos4$\frac{α}{2}$.
解答 证明:2(1+cosα)-sin2α
=2×2$co{s}^{2}\frac{α}{2}$-1+cos2α
=4$co{s}^{2}\frac{α}{2}$-1+($2co{s}^{2}\frac{α}{2}-1$)2
=4$co{s}^{2}\frac{α}{2}$-1+($2co{s}^{2}\frac{α}{2}-1$)2+$4co{s}^{4}\frac{α}{2}-4co{s}^{2}\frac{α}{2}+1$
=4cos4$\frac{α}{2}$.
∴2(1+cosα)-sin2α=4cos4$\frac{α}{2}$.
点评 本题考查三角函数恒等式的化简证明,是中档题,解题时要认真审题,注意二倍角公式和同角三角函数关系式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若sinα,cosα是关于x的方程4x2+2x+3m=0的两根,则m的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{2}$ |
6.已知向量$\overrightarrow{AB}$=(3,-1),$\overrightarrow{ON}$=(-2,0),若$\overrightarrow{AB}$=$\overrightarrow{MN}$,则$\overrightarrow{OM}$等于( )
| A. | (1,-1) | B. | (5,-1) | C. | (-5,1) | D. | (1,-5) |
20.已知数列{an}为等差数列,且a5+a7+a9+a11+a13=80,则a14+a16-a21=( )
| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
4.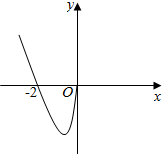 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(0,2) |