题目内容
14.定义在实数集R上的函数f(x),如果存在函数g(x)=Ax+B(A,B为常数),使得f(x)≥g(x)对一切实数x都成立,那么称g(x)为函数f(x)的一个承托函数.下列说法正确的有:①③.(写出所有正确说法的序号)①对给定的函数f(x),对承托函数可能不存在,也可能有无数个;
②定义域和值域都是R的函数f(x),不存在承托函数;
③g(x)=ex为函数f(x)=ex的一个承托函数;
④函数f(x)=$\frac{x}{{x}^{2}+x+1}$不存在承托函数.
分析 函数g(x)=Ax+B(A,B为常数)是函数f(x)的一个承托函数,即说明函数f(x)的图象恒在函数g(x)的上方(至多有一个交点)①举例可以说明,如f(x)=sinx,则g(x)=B(B<-1)就是它的一个承托函数,且有无数个,反例如y=tanx或y=lgx就没有承托函数.
②如取f(x)=2x+3,即可看出其不符合,故错.
③要说明g(x)=ex为函数f(x)=ex的一个承托函数,即证明F(x)=ex-2x的图象恒在x轴上方.
④先求函数的值域,从而可知函数有无数个承托函数.
解答 解:①如f(x)=sinx,则g(x)=B(B<-1)就是它的一个承托函数,且有无数个,再如y=tanx.y=lgx就没有承托函数,∴命题①正确;
②f(x)=2x+3的定义域和值域都是R,存在一个承托函数y=2x+1,故命题②不正确;
③令F(x)=ex-ex,F′(x)=ex-e=0,得x=1,
当x<1时,F′(x)<0,F(x)单调递减,
当x>1时,F′(x)>0,F(x)单调递增,
∴当x=1时,F(x)取最小值=0,
∴f(x)≥g(x)对一切实数x都成立
∴③正确;
④设函数$f(x)=\frac{x}{{x}^{2}+x+1}$=y,则yx2+(y-1)x+y=0
若y=0,则x=0,成立
若y≠0,则△≥0,即(y-1)2-4y2≥0且y≠0,
∴(3y-1)(y+1)≤0且y≠0,
∴-1≤y<0或$0<y≤\frac{1}{3}$
综上知,$-1≤y≤\frac{1}{3}$
∴y=A(A≤-1)就是它的一个承托函数,且有无数个;
∴命题④不正确;
故答案为:①③
点评 本题是新定义题,考查对题意的理解和转化的能力,要说明一个命题是正确的,必须给出证明,对于存在性命题的探讨,只需举例说明即可,对于不正确的命题,举反例即可,有一定的综合性.

| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
| 学生 | A | B | C | D | E |
| 数学(分) | 89 | 91 | 93 | 95 | 97 |
| 物理(分) | 87 | 89 | 89 | 92 | 93 |
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,求选中的同学中物理成绩高于90分的恰有1人的概率.
(附:回归方程$\widehat{y}$=bx+$\widehat{a}$中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$)
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{6}$ |
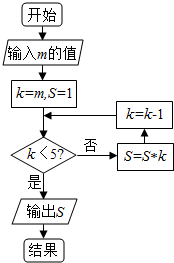
| A. | 7 | B. | 42 | C. | 210 | D. | 840 |